割り算アルゴリズムとグレブナー基底
〜連立方程式でナンプレを解こう!〜
1. 1変数多項式の割り算
高校数学IIで学習する1変数多項式の割り算を復習する.まず1変数多項式の割り算の筆算の方法を見る.筆算は次の手順で行う:1変数多項式$f$を$g$で割る場合,-
$f$の最大次数が$g$の最大次数以上なら,$g$に足りない式を掛けて$f$から引くことで$f$の最大次数の項を打ち消し,ステップ(2)へ.
-
打ち消した後の式の最大次数が$g$の最大次数以上なら,その式に対してステップ(1)へ.小さければ筆算を終える.
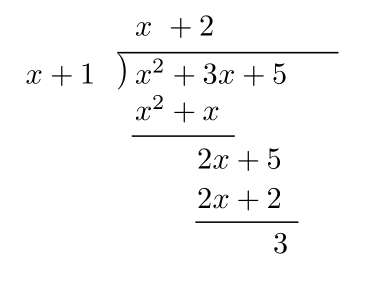
$f=q \times g + r$である,
$r$の次数は$g$の次数より小さい,
2. 2変数多項式の割り算
次に変数をひとつ増やして,$x$と$y$の2変数多項式の割り算を考えてみよう. 1変数のときと同じように筆算してみると少し問題が起こる.実際,$x^3$を$x^2+y^2$で割る筆算を1変数多項式の場合と同様にしてみる. \[ \]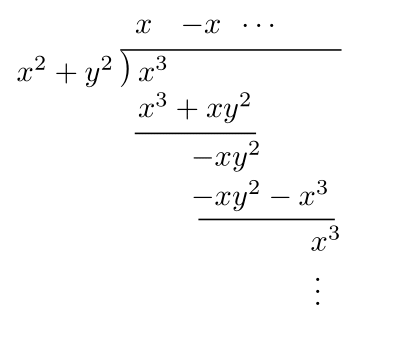
-
$x$の次数が大きい方の単項式が大きい.
-
$x$の次数が同じであれば,$y$の次数が大きい方の単項式が大きい.
-
${\rm LM}(f)$が${\rm LM}(g)$で割り切れるなら,$g$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し,打ち消した後にできる式に対してステップ(1)に戻る.割り切れないならステップ(2)へ.
-
${\rm LM}(f)$の項を余りに移動させ,残った式が$0$でないならその式に対してステップ(1)に戻る.$0$だったら筆算を終える.
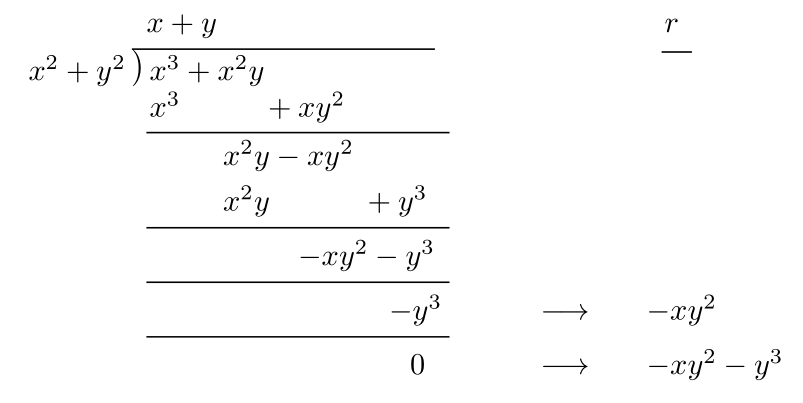
$f=q \times g + r$である,
$r$の各項は${\rm LM}(g)$で割り切れない,
3. $n$変数多項式の割り算
1変数多項式の割り算を2変数多項式の割り算に拡張する場合は色々改善する点があったが,3変数 多項式の割り算は2変数多項式の割り算をそのまま拡張すればよい. 変数$x,y,z$の$3$変数多項式を考える. まず単項式の大小関係を次のルールで決める.-
$x$の次数が大きい方の単項式が大きい.
-
$x$の次数が同じであれば,$y$の次数が大きい方の単項式が大きい.
-
$x$と$y$のそれぞれの次数が同じであれば,$z$の次数が大きい方の単項式が大きい.
4. 複数の多項式での割り算
さらに多項式の割り算を拡張していく.ここまではひとつの多項式で割ることを考えてきたが,複数の多項式で割ることも考えられる. 実際は次のように拡張する.$f = q_1g_1+q_2 g_2 +\cdots + q_s g_s +r$である,
$r$の各項は${\rm LM}(g_1), {\rm LM}(g_2),\ldots, {\rm LM}(g_s)$のいずれでも割り切れない,
(おまじない)$q_i$が$0$でないならば,${\rm LM}(f)$は辞書式順序に関して${\rm LM}(q_i g_i)$以上である.
${\rm LM}(f)$が${\rm LM}(g_1)$で割り切れるなら,$g_1$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し,打ち消した後にできる式に対してステップ(1)に戻る.割り切れないならステップ(2)へ.
${\rm LM}(f)$が${\rm LM}(g_2)$で割り切れるなら,$g_2$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し,打ち消した後にできる式に対してステップ(1)に戻る.割り切れないならステップ(3)へ.
- $\vdots$
${\rm LM}(f)$が${\rm LM}(g_s)$で割り切れるなら,$g_s$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し,打ち消した後にできる式に対してステップ(1)に戻る.割り切れないならステップ(r)へ.
${\rm LM}(f)$の項をあまりに移動させ,残った式が$0$でないならその式に対してステップ(1)に戻る.$0$だったら筆算を終える.
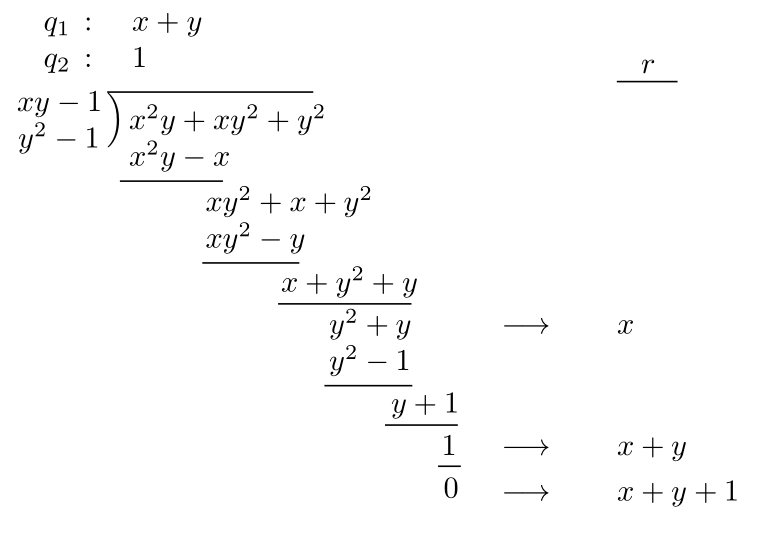
5 割り算の連立方程式への応用
割り算アルゴリズムの連立方程式への応用を紹介する. 連立方程式を解く極意は,いくつかの式をうまく組み合わせて変数が少ない式を見つけることである. 例えば,連立方程式 \[ \begin{cases} f_1=xy+z^2-2=0 \\ f_2=x^2-yz=0\\ f_3=xz-y^2=0 \end{cases} \] を考えてみよう. 実は変数をうまく消せば \[ z^4-3z^2+2=0 \] が得られる. どうすればこの式を見つけることができるだろうか.おそらくかなり時間をかけても見つけることは難しいだろう.しかし,ブッフバーガーアルゴリズムという多項式の割り算に関するアルゴリズムを使えば見つけることができる.3つの多項式$f_1,f_2,f_3$に関するブッフバーガーアルゴリズムを簡単に説明する.-
$f_1,f_2,f_3$から適当に2つ選ぶ(例えば$f_1,f_2$).
-
選んだ2つの多項式の先頭単項式を打ち消した式$f$を考える (${\rm LM}(f_1)=xy$と${\rm LM}(f_2)=x^2$だから$x^2y$(最小公倍元)に揃えて打ち消す,つまり$f=xf_1-y f_2$).
-
$f$を$f_1,f_2,f_3$で割った余りを$r$とする($r=-2x+2y^2z$).
-
$r \neq 0$ならば$f_4=r$とし,ステップ(1)を$f_1,f_2,f_3,f_4$で始める(次は$f_1$と$f_4$を選ぶなど).
-
ステップ(1)からステップ(2)の操作をどの2つの多項式を選んでも$r=0$となるまで続ける.
- $3$変数$x,y,z$の連立方程式を式変形して$z$だけの式が作れるならば,そのような式はグレブナー基底から見つけられる.
- グレブナー基底の中に$z$だけの式がないのなら,どう式変形しても$z$だけの式を作ることはできない.
- 連立方程式の解が$(x,y,z)=(a,b,c)$の1個しかない場合は$x-a,y-b,z-c$という形の式が必ずグレブナー基底に現れる.
-
$f_1,f_2$から$f_4=-2x+2y^2z$を作る.
-
$f_1,f_4$から$f_5=-2y^3z-2z^3+4$を作る.
-
$f_3,f_4$から$f_6=-2y^2z^2+2y^2$を作る.
-
$f_5,f_6$から$f_7=4y^3+4z^3-8z$を作る.
-
$f_5,f_7$から$f_8=8z^4-24z^2+16$を作る.
6. ナンプレを連立方程式で解いてみる
最後に,グレブナー基底を使ってナンプレを解いてみる.ナンプレのルールを知らない人は,まず調べてみよう. ナンプレの各マス目に対し, $81$個の変数$x_i$を以下のように対応させる.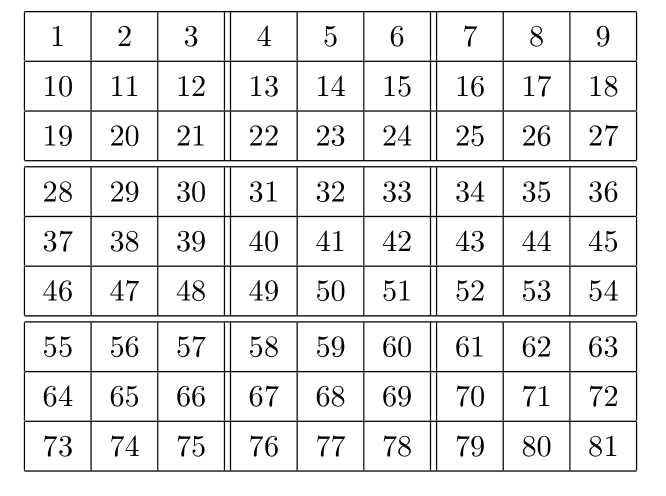
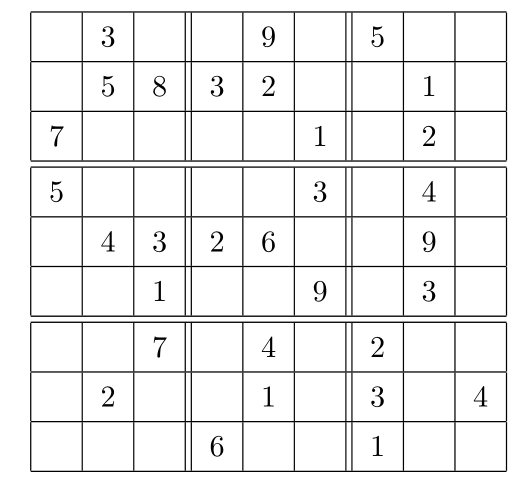
- すべての$F(x_j)=0$,
- 同じ列,行,ブロックのどれかにいるすべての$i$と$j$に対する$G(x_i,x_j)=0$,
- すべての$H(x_i)=0$
