数え上げで求める格子凸多角形の面積と格子凸多面体の体積
1. 格子凸多角形の面積
$xy$平面の図形$\mathcal{P}$が凸であるとは， $\mathcal{P}$の中にあるどんな2点を結んでも，その線分は$\mathcal{P}$の中にあるときにいう．
今，下図のような格子凸多角形の面積を求めたいとしよう．
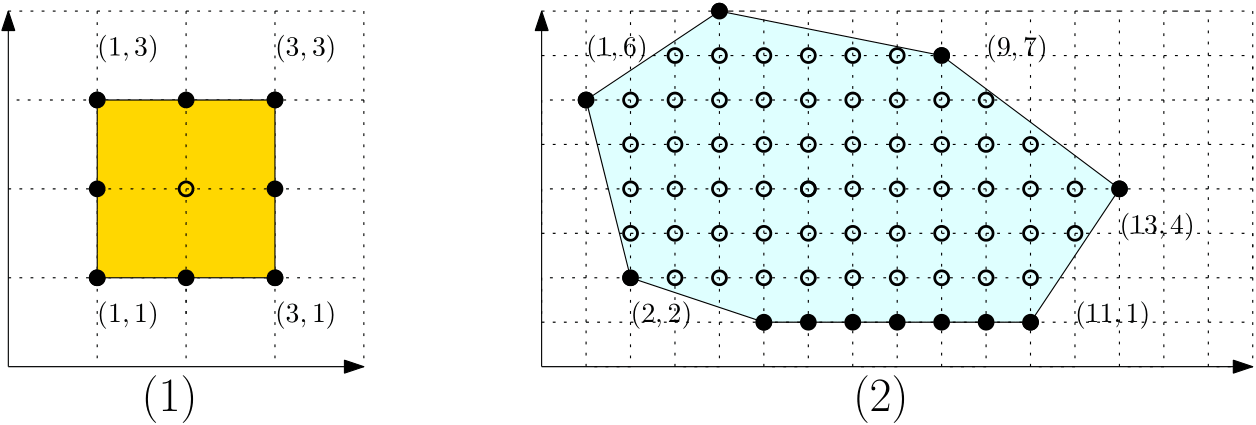
ピックの公式
格子凸多角形$\mathcal{P}$に対し，
先ほどの例で計算してみる．
- $i$を$\mathcal{P}$の内部にある格子点の個数（白丸の個数）とする．
- $b$を$\mathcal{P}$の境界にある格子点の個数（黒丸の個数）とする．
- $i=1,b=8$なので \[\mbox{面積}=1+\dfrac{8}{2} -1=4.\]
- $i=56,b=12$なので \[\mbox{面積}=56+\dfrac{12}{2}-1=61.\]
命題
すべての頂点が格子点となるような正三角形（格子正三角形）は存在しない．
証明
格子正三角形が$xy$平面内に存在したとする．平行移動や対称性により，$(0,0)$と$(a,b)$（ただし$a, b$は非負整数で同時に$0$とはならない）を頂点に持つと仮定して良い．このとき，三平方の定理からこの正三角形の1辺の長さは$\sqrt{a^2+b^2}$である．するとこの正三角形の面積は
\[
\frac{\sqrt{3}}{4} \cdot (\sqrt{a^2+b^2})^2=\frac{\sqrt{3}}{4}(a^2+b^2)
\]
となる．$a^2+b^2$は自然数なので，この面積は無理数となる．しかし，ピックの公式より，格子多角形の面積は必ず有理数となるので矛盾する．よって格子正三角形は$xy$平面内に存在しない．
$xy$平面上の点$(a,b)$は，$a$と$b$がともに有理数のとき，有理点と呼ばれる．すべての頂点が有理点となる凸多角形のことを有理凸多角形と呼ぶ．有理凸多角形は何倍かに相似拡大すると格子凸多角形となる．特に有理正三角形は格子正三角形となる．
すると，先ほどの命題から次の命題が得られる．
命題（1991年大阪大学）
$xy$平面内において有理正三角形は存在しない．
2. 格子凸多面体の体積
次にピックの公式を$3$次元の場合に拡張できないか考えてみよう． $xyz$空間の図形$\mathcal{P}$が凸であるとは， $\mathcal{P}$の中にあるどんな2点を結んでも，その線分は$\mathcal{P}$の中にあるときにいう． 特に凸な多面体のことを凸多面体と呼ぶ． 一方，$xyz$空間の点$(x,y,z)$が格子点であるとは，$x,y,z$がすべて整数であるときに言う． さらに，すべての頂点が格子点であるときような凸多面体を格子凸多面体という．それではピックの公式と同様に格子凸多面体の体積が格子点の数え上げで計算できるか考えてみる． 実は，ピックの公式をそのまま拡張することはできない．それを確認するために次の例を考えてみよう．
例
以下の四面体を考える．
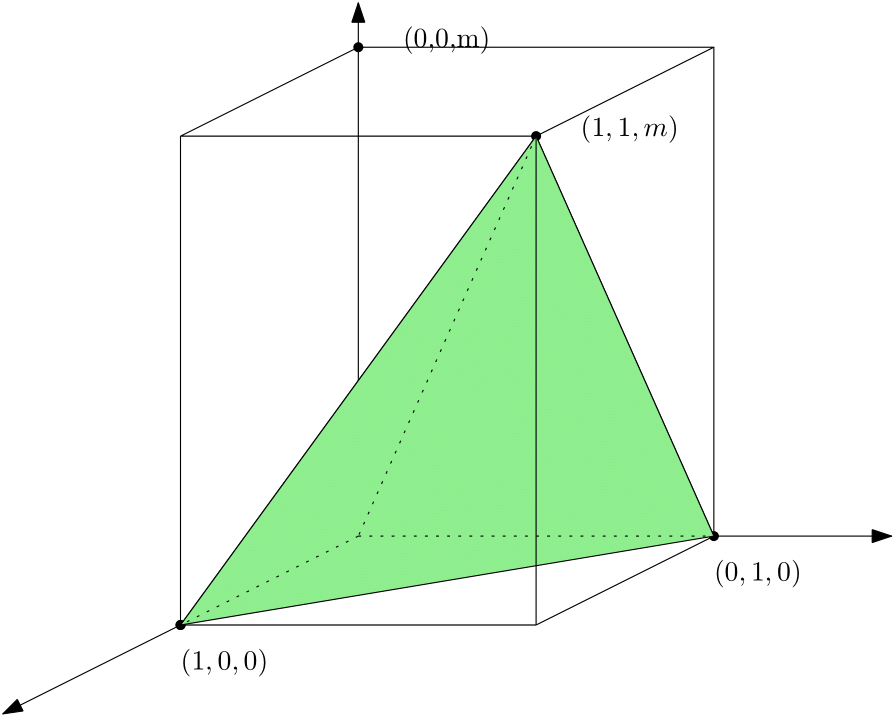この四面体の体積は$\dfrac{m}{6}$（$m$が大きくなると体積が大きくなる）である．
一方，内部と境界にある格子点の個数はそれぞれ$0$個と$4$個（$m$が大きくなっても変わらない）である．
すると含まれる格子点の個数だけでは体積が一つに定まらない，つまり計算できないことがわかる．
ではどのようにすれば格子点の数え上げで格子凸多面体の体積を計算することができるだろうか．
そのためには，凸多面体の「膨らまし」を考える．格子凸多面体$\mathcal{P}$と自然数$n$に対し，$L_{\mathcal{P}}(n)$を$\mathcal{P}$を$n$倍に膨らました$n\mathcal{P}$に含まれる格子点の個数とする．
例で確認してみよう．わかりやすいように凸多角形で考える．
例
下図のような長さ$1$の格子正方形$\mathcal{P}$を考える．
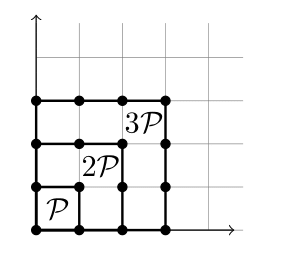すると，
\[
L_{\mathcal{P}}(1)=4, L_{\mathcal{P}}(2)=9, L_{\mathcal{P}}(3)=16, \ldots, L_{\mathcal{P}}(n)=(n+1)^2, \ldots
\]
となる．
この例のように格子凸多角形だと$L_{\mathcal{P}}(n)=x^2+2n+1$のように$L_{\mathcal{P}}(n)$は$2$次の多項式になっている．実は格子凸多面体の場合は$L_{\mathcal{P}}(n)$は$3$次の多項式になっていて，さらにこの多項式を計算することで体積を計算することができる．
エルハートの基本定理
$xyz$空間の格子凸多面体$\mathcal{P}$に対し，$L_{\mathcal{P}}(n)$は
\[
L_{\mathcal{P}}(n)=an^3+bn^2+cn+1
\]
という形をしている．特に$L_{\mathcal{P}}(n)$の$3$次の係数，つまり$a$は$\mathcal{P}$の体積と一致する．
この多項式$L_{\mathcal{P}}(n)$を$\mathcal{P}$のエルハート多項式と呼ぶ．
エルハート多項式は$n\mathcal{P}$の全体に含まれる格子点の個数を数え上げる多項式であるが，この多項式から$n\mathcal{P}$の内部と境界の格子点の個数を分けて計算することもできる．
エルハート・マクドナルド相互法則
$xyz$空間の格子凸多面体$\mathcal{P}$のエルハート多項式が
\[
L_{\mathcal{P}}(n)=an^3+bn^2+cn+1
\]
と書けるとき，
\[(n\mathcal{P}\mbox{の内部に含まれる格子点の個数})=an^3-bn^2+cn-1\]
となる．よって
\[(n\mathcal{P}\mbox{の境界に含まれる格子点の個数})=2bn^2-2\]
である．
したがって体積を計算するには$a$を求めればいいので，
$\mathcal{P}$と$2\mathcal{P}$の境界と内部の格子点の個数が分かれば連立方程式を解いてエルハート多項式が求まり，体積も求まる．
例
さっきの例で確かめてみる．
この四面体のエルハート多項式は
\[
L_{\mathcal{P}}(n)=\dfrac{m}{6}n^3+n^2+\cfrac{12-m}{6}n+1
\]
となる．
計算するのは大変だがこの多項式から$\mathcal{P}$の体積は$\frac{m}{6}$であることがわかる．
3. 一般次元の凸多面体
$4$次元以上の凸多面体を考えていきたい． そのために，まず$4$次元以上の空間がどういったものか考える．$xy$平面や$xyz$空間は$\mathbb{R}^2$や$\mathbb{R}^3$と書くことがある．この$\mathbb{R}$という記号はすべての実数の集合である． では$\mathbb{R}^2$や$\mathbb{R}^3$は何を意味しているかというと，$\mathbb{R}^2$は２つの実数の組$(x,y)$を集めた集合，$\mathbb{R}^3$は３つの実数の組$(x,y,z)$を集めた集合であり，それぞれ$2$次元実空間や$3$次元実空間と呼んだりする．つまり$\mathbb{R}^2$は2つ組のデータの集まり，$\mathbb{R}^3$は3つ組のデータの集まりであり，$xy$平面や$xyz$空間はそれを視覚的に見たものである．では「見る」ことを忘れれば，4つ組のデータの集まり，5つ組のデータの集まり，つまり$\mathbb{R}^4$や$\mathbb{R}^5$を考えることができる．もっと一般に$d$個の実数の組$(x_1,x_2,\ldots,x_d)$を集めた集合$\mathbb{R}^d$を考えることができる．この$\mathbb{R}^d$を$d$次元実空間と呼ぶ．データの集まりとして考えると，実用的に2つ組や3つ組のデータだけでは足りない．つまり$\mathbb{R}^4, \mathbb{R}^5, \mathbb{R}^6,\ldots$を考える必要がある．$\mathbb{R}^4, \mathbb{R}^5, \mathbb{R}^6,\ldots$は書けないし，見えないが，そこの中にある集合を``図形"だと思って数学者は考えている．
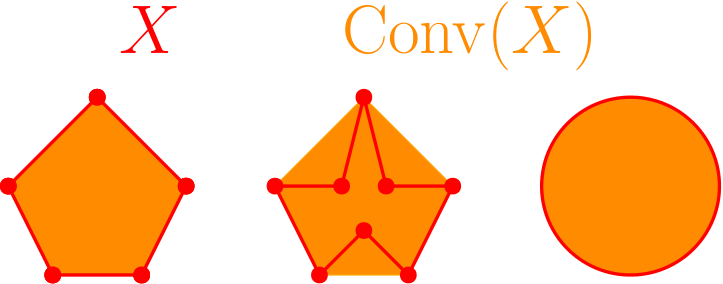
次に凸多角形の厳密な定義を考えてみる． $xy$平面でいくつか（無限個でも可）の点の集合$X$に対し， $X$を含む一番小さい凸集合のことを$X$の凸閉包と呼び，${\rm Conv}(X)$と書く． 下図のように凸閉包は$X$全体を凹まないように囲って内側を塗りつぶすイメージである．
定義
$\mathbb{R}^2$の中の集合$\mathcal{P}$は有限個の点の集合$X$を使って$P={\rm Conv}(X)$と書けるとき，凸多角形であるという．
また$\mathcal{P}={\rm Conv}(X)$となる，もっとも少ない点の集合$X$を$\mathcal{P}$の頂点集合といい，その中のそれぞれの点を$\mathcal{P}$の頂点と言う．
例えば，五角形は下図の左２つのような有限個の点の集合の凸閉包として書けるので凸多角形である．また中央の図の5点はこの五角形を表すための最小の点の集合であるので，この5点が頂点であり，今まで思っていた「頂点」と一致していることがわかる．一方，円は凸集合であるが，この円を凸閉包で書こうとすると円周上の点を全て集める必要があり，これは無限個ある．凸多角形の定義の中の「有限個の点」という条件が凸多角形の定義の本質である．
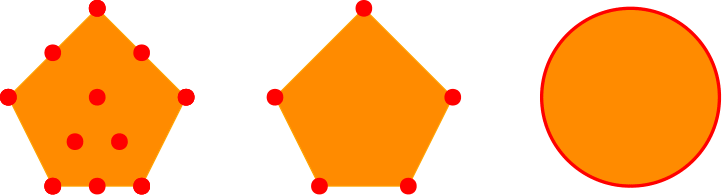
定義
$\mathbb{R}^d$の中の集合$\mathcal{P}$は有限個の点の集合$X$を使って$P={\rm Conv}(X)$と書けるとき，凸多面体であるという．
また$\mathcal{P}={\rm Conv}(X)$となる，もっとも少ない点の集合$X$を$\mathcal{P}$の頂点集合といい，その中のそれぞれの点を$\mathcal{P}$の頂点と言う．
例えば，$\mathbb{R}^3$内で各座標が$0$か$1$のすべての点の集合
\[
X=\{(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),(1,0,1),(0,1,1),(1,1,1)\}
\]
に対し，${\rm Conv}(X)$は長さ$1$の立方体である．同様に，$\mathbb{R}^d$内で各座標が$0$か$1$のすべての点の集合$X$に対し，${\rm Conv}(X)$は長さ$1$の超立方体と呼ばれる．
基本的に$4$次元以上の凸多面体を見ることはできないが， $4$次元超立方体のイメージする方法を紹介する． そのために，$2$次元の立方体（これは正方形）から$3$次元立方体を作る方法を考える． 今，正方形を一つ準備して，その正方形を2つにコピーし，この２つの正方形の頂点をそれぞれ辺で結ぶ．すると立方体の骨組みのようなものができるであろう．
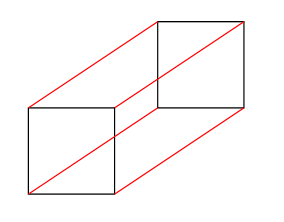
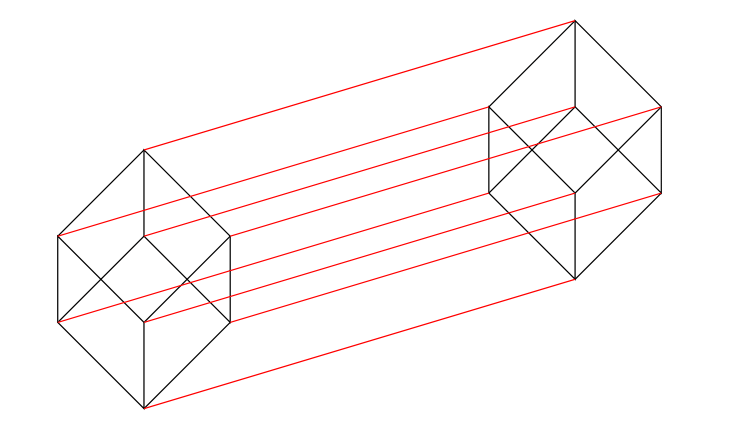
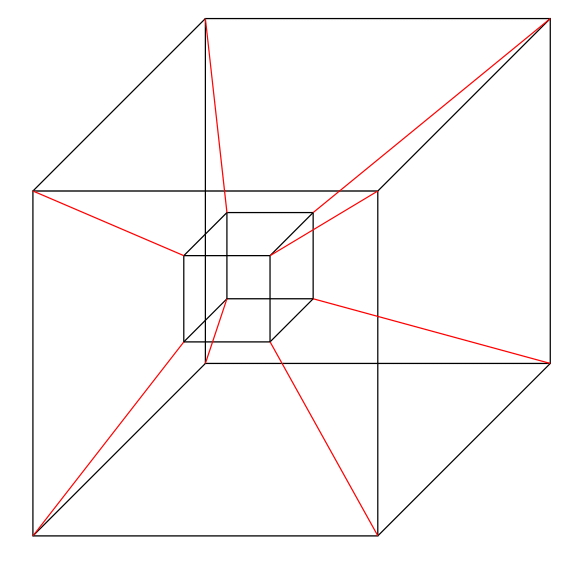
3'. もう一つの凸多面体の定義
一般次元の凸多面体を定義する方法はもう一つある．凸多角形は下の図のように$xy$平面のいくつかの直線（下図の三角形$\mathcal{P}$の場合$L_1,L_2,L_3$）で囲まれた領域で表現できる．直線は一般に$ax+by=c$という式で表される．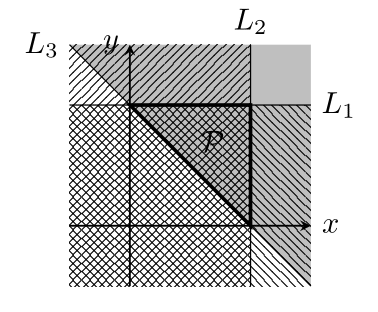
4. エルハート理論
$d$次元凸多面体の体積を厳密に定義することはここではやめて，超立方体を使って体積を定義する．$xy$平面では長さ$1$の正方形の面積は$1$，$xyz$空間では長さ$1$の立方体の体積は$1$であった．そこで，$d$次元の長さ$1$の超立方体の体積を$1$と定義し，一般の凸多面体の体積はこの超立方体が何個入るか，ということで定義する．$4$次元以上の凸多面体は描けないし，目に見えないため，体積を計算することは想像しにくいだろう．しかし，一般次元の格子凸多面体の場合，$3$次元のときと同様に格子点の数え上げであるエルハート多項式を計算することで体積を求めることができる．
$\mathbb{R}^d$の点は，すべての座標が整数のとき，格子点と呼ばれる． すべての頂点が格子点となる$d$次元凸多面体を格子凸多面体と呼ぶ． また凸多面体$\mathcal{P}$の各点のすべての座標を$n$倍にしたものを$n\mathcal{P}$と書く． このとき，$L_{\mathcal{P}}(n)$を$n\mathcal{P}$に含まれる格子点の個数とする．
エルハートの基本定理
$\mathbb{R}^d$の$d$次元格子凸多面体$\mathcal{P}$に対し，$L_{\mathcal{P}}(n)$は
\[L_{\mathcal{P}}(n)=a_d n^d+a_{d-1} n^{d-1}+\cdots+a_1 n+1\]
という形をしている．
特に，$L_{\mathcal{P}}(n)$の$d$次の係数，つまり$a_d$は$\mathcal{P}$の体積と一致する．
この多項式$L_{\mathcal{P}}(n)$を$\mathcal{P}$のエルハート多項式と呼ぶ．
さらに$3$次元の場合と同様で次の定理が成り立つ．
エルハート・マクドナルド相互法則
$xyz$空間の格子凸多面体$\mathcal{P}$のエルハート多項式が
\[L_{\mathcal{P}}(n)=a_d n^d+a_{d-1} n^{d-1}+\cdots+a_1 n+1\]
と書けるとき，
\[(n\mathcal{P}\mbox{の内部に含まれる格子点の個数})=a_d n^d-a_{d-1} n^{d-1}+\cdots+(-1)^{d-1} a_1 n+(-1)^d\]
となる．
この二つの定理を組み合わせると，$\mathcal{P}, 2\mathcal{P}, 3\mathcal{P},\ldots, [\frac{d+1}{2}] \mathcal{P} $の境界と内部の格子点の個数が分かれば連立方程式を解いてエルハート多項式が求まり，体積も求まる．
このエルハート多項式を研究する分野をエルハート理論といい，格子凸多面体の研究の中心の一つになっている．