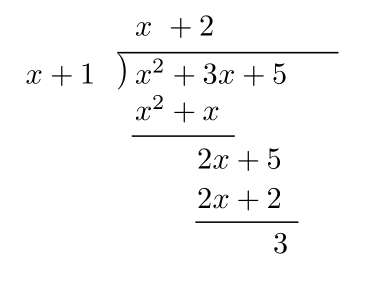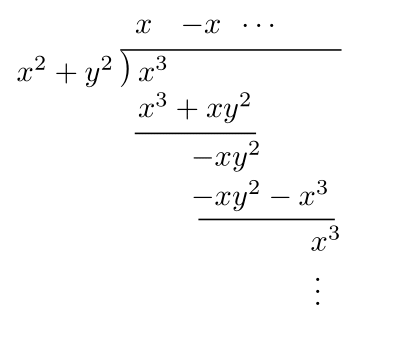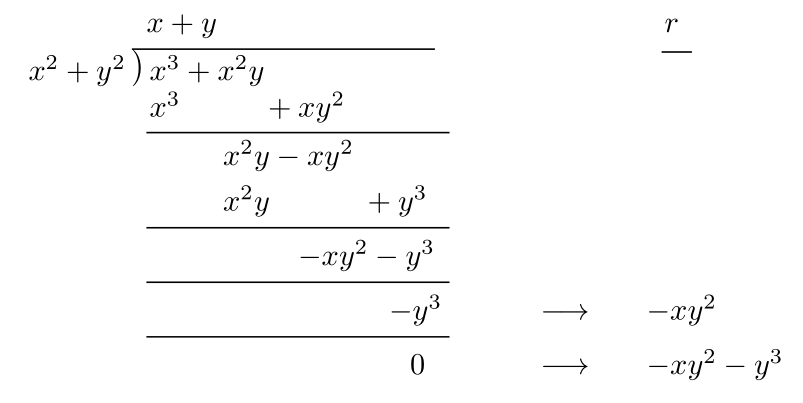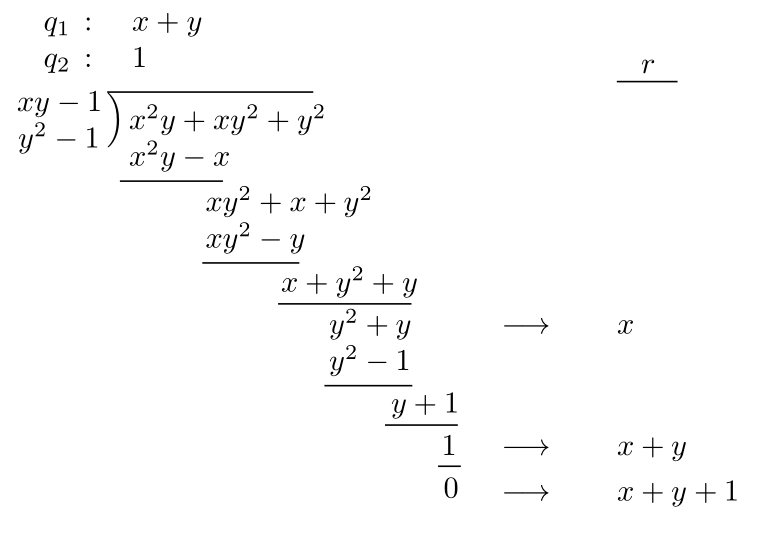割り算アルゴリズムとグレブナー基底
〜連立方程式でナンプレを解こう！〜（ロング版）

0. はじめに：大学数学では何をするのか

高校までの数学では，計算や公式を使うことが中心に見えるかもしれない． たとえば，方程式を解く，因数分解する，図形の面積を求める，微分や積分を計算する，といった内容である． もちろん，計算は数学にとって非常に重要である． しかし，数学は単に公式を覚えて数を代入するだけの学問ではない．

大学数学では，身近な計算や概念について，まず「それは何をしているのか」を定義として捉え直す． そして，その定義をもとに，別の対象やより広い世界へ拡張していく． この「定義し直す」「拡張する」という考え方は，大学数学の基本的な姿勢のひとつである．

今回の講義では，小学校で学んだ「割り算」を出発点にする． 自然数の割り算を定義し直し，それを1変数多項式の割り算へ拡張し，さらに多変数多項式，複数の多項式での割り算へと拡張していく． その途中で，割る順番によって余りが変わるという新しい問題が現れる． この問題を解決するために登場するのがグレブナー基底である．

また，数学では「現象を式に翻訳する」ことも大切である． 高校数学でも，図形を方程式で表すことを学ぶ． たとえば，円を \[ x^2+y^2=1 \] という式で表せば，図を描かなくても式の計算だけでその図形を調べることができる． この考え方は，平面上の図形だけでなく，目に見えない高次元の図形や，ナンプレのようなパズルにも応用できる．

1. 自然数の割り算

小学生の頃学習した割り算を思い出すと，例えば，$5 \div 2$は商$2$余り$1$であった．他にも$13 \div 5$は商$2$余り$3$である．算数では具体例を使って割り算や商，余りを説明していたが，数学的に厳密に定義できるだろうか．ただし，ここで考えたいのは，$5 \div 2= 2.5$のように小数点以下まで考える割り算ではなく，余りも考慮した自然数の中だけの割り算である．さて，割り算の見方を変えると，「$5 \div 2$は商$2$余り$1$」からは数式 \[ 5= 2 \times 2 +1 \] が得られ， 「$13 \div 5$は商$2$余り$3$」からは \[ 13=2 \times 5 +3 \] が得られる．ここで「余り」がいつでも割る数より小さいことに注意する． これは「これ以上割れない」ということを意味する． このような表示を与えることを「割り算」と定義することで，数式を使って「割り算」を説明することができる．つまり，割り算の厳密な定義は以下の通りである： 自然数の割り算は筆算すれば必ず答え（商と余り）を求めることができたことを思い出そう．これは割り算の答えがいつでも存在することを意味する．さらに，そのときの答えはひとつしかなかったことを思い出そう．つまり，次の事実が成り立つ． 数学では定義も大事だが，その定義に対して

• 答えの存在
• 答えの一意性（ひとつしかないこと）
• 答えを見つける方法（アルゴリズム）

も重要である．

2. 1変数多項式の割り算

数や文字についての掛け算だけで作られた式を単項式という． 例えば，$2$や$-3x$，$x^2y$などである．単項式に対して

• 掛けられている文字の個数を次数，
• 文字を取り除いた数を係数

という．例えば，$2, -3x, x^2y$の次数はそれぞれ$0, 1, 3$であり係数は$2, -3, 1$である．いくつかの単項式の足し算で表せる式（ただし，$2x+3x$は$5x$のようにひとつにまとめられる部分があればひとつにまとめた最も簡単な式）を多項式という．例えば，$2+(-3x)+x^2y$は多項式である． 多項式に対して

• 足された各単項式のことをその多項式の項，
• 各項のうちで最も大きい次数を，その多項式の次数

という．例えば，多項式$2+(-3x)+x^2y$に対して， $2,-3x,x^2y$はこの多項式の項であり，次数は$3$である．文字の種類が$1$種類（以下）しかない多項式のことを$1$変数多項式，$2$種類（以下）しかない多項式のことを$2$変数多項式，もっと一般に$n$種類（以下）しかない多項式のことを$n$変数多項式という．文字は$4$種類以下なら$x,y,z,w$の順で使うことが多い．$n$変数なら$x_1,x_2,\ldots,x_n$という文字を使う． それでは高校数学IIで学習する1変数多項式の割り算を定義する．そのために，1変数多項式の割り算の筆算の方法を見る．筆算は次の手順で行う：1変数多項式$f$を$g$で割る場合，

• $f$の最大次数が$g$の最大次数以上なら，$g$に足りない式を掛けて$f$から引くことで$f$の最大次数の項を打ち消し，ステップ(2)へ．

• 打ち消した後の式の最大次数が$g$の最大次数以上なら，その式に対してステップ(1)へ．小さければ筆算を終える．

実際，具体例で考えると次の計算を行う． $x^2+3x+5$を$x+1$で割ることを考える．すると筆算は以下のように書ける． \[ \] このとき，$x+2$が商，$3$が余りとなっている．よって数式 \[ x^2+3x+5=(x+1)(x+2)+3 \] が得られる． 実はこの表示を得ることが割り算の目的である．この筆算を元に1変数多項式の割り算を厳密に定義すると次の通りになる． 自然数の割り算では余りの条件は「割る数より小さい」であった．これは「これ以上割ることができない」を意味している．1変数多項式の割り算の場合，この条件が(2)の「余り$r$の次数は割る多項式$g$より次数が小さい」となる． 筆算を使うことで$1$変数多項式の割り算は必ず答えを求めることができる．特に，その答えはひとつしかない．つまり，自然数の割り算と同様に次の事実が成り立つ． よって1変数多項式の割り算も

• 答えの存在
• 答えの一意性（ひとつしかないこと）
• 答えを見つける方法（アルゴリズム）

がわかった．

3. 2変数多項式の割り算

それでは変数をひとつ増やして，$x$と$y$の2変数多項式の割り算を考えてみよう． 1変数のときと同じように筆算してみると少し問題が起こる．実際，$x^3$を$x^2+y^2$で割る筆算を1変数多項式の場合と同様にしてみる． \[ \] $1$変数の場合，$x^2$や$x^3$のような次数が$2$や$3$の単項式はこれらしかない． しかし，$2$変数の場合$x^2$や$y^2$のように次数が同じだけど異なる単項式が存在する．その結果，この筆算のように，次数が最大の項をひとつ打ち消しても，次数が下がらず，筆算が終わらないことが起こる．この問題を解決するために，次数全体を比べるのではなく，それぞれの変数の次数ごとに大きさを比較して，すべての単項式に順番（大小）をつけることを考える． 単項式の大小関係を次のルールで決める．

• $x$の次数が大きい方の単項式が大きい．

• $x$の次数が同じであれば，$y$の次数が大きい方の単項式が大きい．

例えば，$1 \lt y \lt y^2 \lt x \lt x y^2 \lt x^2 \lt x^3y$のようになる． この大小関係を辞書式順序という．注意して欲しいのは$y^2 \lt x$のように全体の次数が大きかったとしても辞書式順序では小さくなる場合があることである．どれだけ次数が高くても，$x$の次数が小さければ小さくなるのである．多項式$f$の一番大きい項の単項式を先頭単項式といい，${\rm LM}(f)$と書くことにする． 例えば，$f=2x^3+x^2y+3xy^2-y^3+1$の辞書式順序で最大の項は$2x^3$なので，${\rm LM}(f)=x^3$である． さて，この辞書式順序を使って，筆算を次のように改良する． 2変数多項式$f$を$g$で割る場合，

• ${\rm LM}(f)$が${\rm LM}(g)$で割り切れるなら，$g$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し，打ち消した後にできる式に対してステップ(1)に戻る．割り切れないならステップ(2)へ．

• ${\rm LM}(f)$の項を余りに移動させ，残った式が$0$でないならその式に対してステップ(1)に戻る．$0$だったら筆算を終える．

1変数の場合ステップ(1)では次数を下げていたが，2変数の場合，辞書式順序に関して大きさを下げている． それでは実際に具体例で考える． 辞書式順序に関して$x^3+x^2 y$を$x^2+y^2$で割ってみる． \[ \] すると \[ x^3+x^2y= (x+y) \times (x^2+y^2) +(-xy^2-y^3) \] なので，商$x+y$，余り$-xy^2-y^3$と考えることができる． この筆算を元に，2変数多項式の割り算を定義すると次の通りになる． 1変数の場合(2)の条件は次数が小さいことを意味しているので，この定義は1変数の場合と同じである．この条件(2)が「これ以上割ることができない」を意味している． 1変数の場合と同様で，筆算を使うことで$2$変数多項式の割り算は必ず答えを求めることができる．特に，その答えはひとつしかない．つまり，次の事実が成り立つ． よって2変数多項式の割り算も

• 答えの存在
• 答えの一意性（ひとつしかないこと）
• 答えを見つける方法（アルゴリズム）

がわかった．

4. $n$変数多項式の割り算

1変数多項式の割り算を2変数多項式の割り算に拡張する場合は色々改善する点があったが，3変数 多項式の割り算は2変数多項式の割り算をそのまま拡張すればよい． 変数$x,y,z$の$3$変数多項式を考える． まず単項式の大小関係を次のルールで決める．

• $x$の次数が大きい方の単項式が大きい．

• $x$の次数が同じであれば，$y$の次数が大きい方の単項式が大きい．

• $x$と$y$のそれぞれの次数が同じであれば，$z$の次数が大きい方の単項式が大きい．

この大小関係も同様に辞書式順序という． 辞書式順序さえ定義できれば筆算アルゴリズムは同じステップで計算できる．割り算の定義も特に変える必要はない． さらに変数を$4$個，$5$個，$6$個とどんどん増やしても，辞書式順序さえ定義できれば筆算アルゴリズムと割り算は同じ定義で大丈夫である．$n$個の変数$x_1,x_2,\ldots,x_n$の$n$変数多項式を考える．このとき， 単項式の大小関係を次のルールで決める．

• $x_1$の次数が大きい方の単項式が大きい．

• $x_1$の次数が同じであれば，$x_2$の次数が大きい方の単項式が大きい．

• $x_1$と$x_2$のそれぞれの次数が同じであれば，$x_3$の次数が大きい方の単項式が大きい．

•   $\vdots$

• $x_1,x_2,\ldots,x_{n-1}$のそれぞれの次数が同じであれば，$x_n$の次数が大き方の単項式が大きい．

この大小関係を$n$変数の辞書式順序という． 一般に，$n$変数多項式の割り算は次のようになる． さらに，筆算から次の事実が成り立つ． よって一般にどんな多項式に対しても，その割り算の

• 答えの存在
• 答えの一意性（ひとつしかないこと）
• 答えを見つける方法（アルゴリズム）

がわかった． 以降は多項式というと，$n$変数多項式を意味しているとする．

5. 複数の多項式での割り算

さらに多項式の割り算を拡張していく．ここまではひとつの多項式で割ることを考えてきたが，複数の多項式で割ることも考えられる． 実際は次のように拡張する． この割り算を実行するために，筆算アルゴリズムを次のように改良する． 多項式$f$を$g_1,g_2,\ldots,g_s$で割る場合，

• ${\rm LM}(f)$が${\rm LM}(g_1)$で割り切れるなら，$g_1$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し，打ち消した後にできる式に対してステップ(1)に戻る．割り切れないならステップ(2)へ．

• ${\rm LM}(f)$が${\rm LM}(g_2)$で割り切れるなら，$g_2$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し，打ち消した後にできる式に対してステップ(1)に戻る．割り切れないならステップ(3)へ．

•   $\vdots$

• ${\rm LM}(f)$が${\rm LM}(g_s)$で割り切れるなら，$g_s$に足りない式を掛けて$f$から引くことで${\rm LM}(f)$を打ち消し，打ち消した後にできる式に対してステップ(1)に戻る．割り切れないならステップ(r)へ．

• ${\rm LM}(f)$の項をあまりに移動させ，残った式が$0$でないならその式に対してステップ(1)に戻る．$0$だったら筆算を終える．

つまり，ひとつの多項式で割る場合は${\rm LM}(g)$で${\rm LM}(f)$が割り切れるかどうかだけ見ていたが，複数の多項式で割る場合，それを${\rm LM}(g_1)$から順に判定していき，どれでも割り切れなかったときにはじめて余りに移動させるのである． この筆算を2変数の場合に試してみよう． $x^2+xy^2+y^2$を$xy-1$と$y^2-1$で割ってみると \[ \] となる． すると \[ f=(x+y) \cdot (xy-1) + 1 \cdot (y^2-1)+(x+y+1) \] となることがわかる． この筆算によって，複数の多項式で割った場合でも，

• 答えの存在
• 答えを見つける方法（アルゴリズム）

がわかる．しかし，「答えの一意性」は実は成り立たない． 例えば， $f=xy^2-x$を$xy-1$と$y^2-1$で割ってみよう． $g_1=xy-1$と$g_2=y^2-1$として筆算すると \[ f=y \cdot (xy-1) + 0 \cdot (y^2-1) + (-x+y) \] となる．しかし，$g_1=y^2-1$と$g_2=xy-1$として筆算すると \[ f=x \cdot (y^2-1) + 0 \cdot (xy-1) + 0 \] となる． つまり割る多項式は変わっていないのに，割る順番を変えて筆算すると商と余りが変わる可能性があることがわかる．実は商が変わることは応用上特に問題はないのだが，余りが変わることが非常に厄介である． どんな順番で割っても余りが一意的になるような多項式の集合は応用的に非常に重要である．そのような多項式の集まりはグレブナー基底と呼ばれる． 上の例だと$xy-1$と$y^2-1$はグレブナー基底ではない．しかし，この式に$x-y$という式を追加することで，グレブナー基底にすることができる．つまりどんな多項式$f$を3つの多項式$xy-1$と$y^2-1$と$x-y$で割っても，割る順番に関わらず余りは一意的である． 実は，多項式の集合はいくつか多項式を追加することでいつでもグレブナー基底にすることができる． 次の節で，このグレブナー基底の作り方と，グレブナー基底の連立方程式への応用を紹介する．

6. 割り算の連立方程式への応用

多項式$f_1,f_2,\ldots,f_s$があったとき，ブッフバーガーアルゴリズムという計算でグレブナー基底を作ることができる．具体的に \[ f_1=xy+z^2-2, f_2=x^2-yz, f_3=xz-y^2 \] という3つの多項式で考えてみよう． このアルゴリズムは次のステップで進む．

• $f_1,f_2,f_3$から適当に2つ選ぶ（例えば$f_1,f_2$）．

• 選んだ2つの多項式の先頭単項式を打ち消した式$f$を考える （${\rm LM}(f_1)=xy$と${\rm LM}(f_2)=x^2$だから$x^2y$（最小公倍元）に揃えて打ち消す，つまり$f=xf_1-y f_2$）．

• $f$を$f_1,f_2,f_3$で割った余りを$r$とする（$r=-2x+2y^2z$）．

• $r \neq 0$ならば$f_4=r$とし，ステップ(1)を$f_1,f_2,f_3,f_4$で始める（次は$f_1$と$f_4$を選ぶなど）．

• ステップ(1)からステップ(2)の操作をどの2つの多項式を選んでも$r=0$となるまで続ける．

このアルコリズムはかなり時間がかかるが，必ず有限回の操作でアルゴリズムが終了する． アルゴリズムが終了したときに追加した多項式を含めたすべての多項式$f_1,f_2,\ldots,f_s,f_{s+1},\ldots,f_t$が実はグレブナー基底となっている． この方法で作ったグレブナー基底は連立方程式に応用できる． 連立方程式を解く極意は，いくつかの式をうまく組み合わせて変数が少ない式を見つけることである． 例えば，連立方程式 \[ \begin{cases} 2x +3y=3 \\ 3x+2y=2 \end{cases} \] の場合，一つ目の式に$3$を掛けて，二つ目の式に$2$を掛けて両辺を引くと$x$が消えて$5y=5$という式が得られる． よって$y=1$となり一つ目の式に代入することで$x=0$がわかる． では連立方程式 \[ \begin{cases} f_1=xy+z^2-2=0 \\ f_2=x^2-yz=0\\ f_3=xz-y^2=0 \end{cases} \] を考えてみよう． 実は変数をうまく消せば \[ z^4-3z^2+2=0 \] が得られる． どうすればこの式を見つけることができるだろうか．おそらくかなり時間をかけても見つけることは難しいだろう．しかしこの式はグレブナー基底の中から見つけることができる．この結果を消去定理と呼ぶ． つまり，グレブナー基底を計算すれば答え，または簡単な式を見つけることができるのである． ただし，その計算量は膨大である．実際，上の$f_1,f_2,f_3$から \[ z^4-3z^2+2=0 \] を見つける場合，

• $f_1,f_2$から$f_4=-2x+2y^2z$を作る．

• $f_1,f_4$から$f_5=-2y^3z-2z^3+4$を作る．

• $f_3,f_4$から$f_6=-2y^2z^2+2y^2$を作る．

• $f_5,f_6$から$f_7=4y^3+4z^3-8z$を作る．

• $f_5,f_7$から$f_8=8z^4-24z^2+16$を作る．

この操作によってようやく欲しい式が見つかる． いつか必ず見つかるが，ペアの選び方によっては見つかるまでかなり時間がかかる場合がある． 手計算では大変だが，Macaulay2と呼ばれるオンラインで使用できるソフトウェア（英文ページ）を使えばグレブナー基底は計算できる． ただし表示されるグレブナー基底は「余分」なものを取り除いた被約グレブナー基底というものである． 上の$f_1,f_2,f_3$に対して被約グレブナー基底を計算すると， \[ z^4-3z^2+2,yz^2-y,y^3+z^3-2z,x-y^2z \] となるコード．特に，この4つの多項式の連立方程式を解けば，元の連立方程式の解を求めることができる． 上の説明は$3$変数で考えたが，一般の$n$変数の場合，辞書式順序で見る最後の変数，つまり$x_n$だけの式をグレブナー基底から見つけることができる．注目したい変数があれば変数の順番を入れ替えればよい．

7. ナンプレを連立方程式で解いてみる

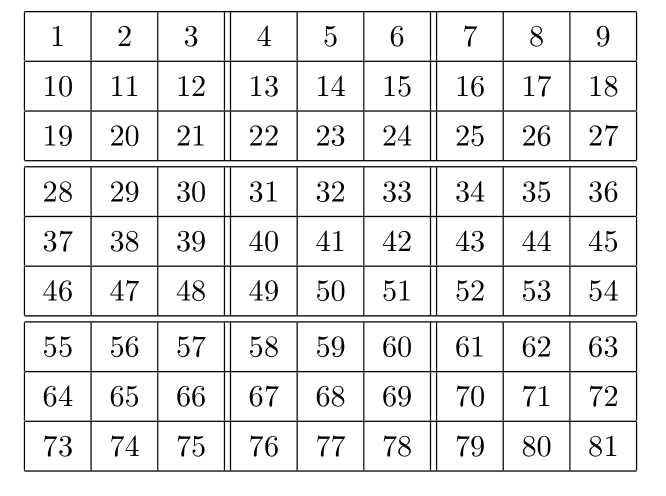
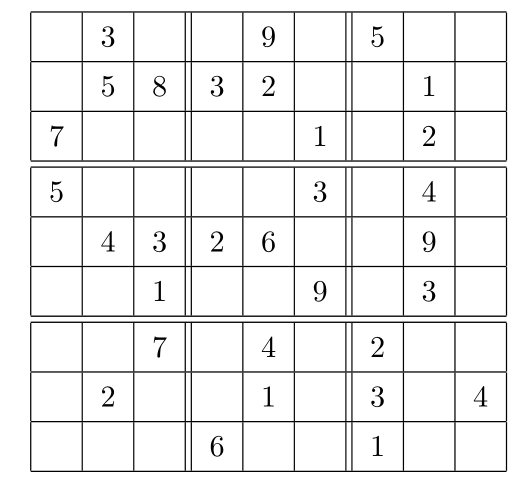
最後に，グレブナー基底を使ってナンプレを解いてみる．ナンプレのルールを知らない人は，まず調べてみよう． ナンプレの各マス目に対し， $81$個の変数$x_i$を以下のように対応させる． そして多項式$F(x_j), G(x_i,x_j)$を次のように定義する． $ j = 1 , \dots, 81$ に対し，\[F(x_j) = (x_j-1)(x_j-2) \cdots (x_j-9) \] $1 \leq i \lt j \leq 81$に対し， \[G(x_i,x_j)=\frac{F(x_i)-F(x_j)}{(x_i-x_j)}\] また初期状態について，$i$のマス目に$a_i$という数字が入っていた場合， \[H(x_i)=x_i-a_i\] とする． 例として，以下のようなナンプレについて考えてみる． このナンプレにおける$H(x_i)$は， \[x_{2}-3,x_{5}-9,x_{7}-5,x_{11}-5,x_{12}-8,x_{13}-3,x_{14}-2,x_{17}-1,\] \[x_{19}-7,x_{24}-1,x_{26}-2,x_{28}-5,x_{33}-3,x_{35}-4,x_{38}-4,\] \[x_{39}-3,x_{40}-2,x_{41}-6,x_{44}-9,x_{48}-1,x_{51}-9,x_{53}-3,x_{57}-7,\] \[x_{59}-4,x_{61}-2,x_{62}-5,x_{65}-2,x_{68}-1,x_{70}-3,x_{72}-4,x_{76}-6,x_{79}-1\] となる． このとき，

• すべての$F(x_j)=0$，
• 同じ列，行，ブロックのどれかにいるすべての$i$と$j$に対する$G(x_i,x_j)=0$，
• すべての$H(x_i)=0$

からなる約1000個の連立方程式を解くとナンプレの答えがわかる． ナンプレは答えが一つしかないので，$x_i=a$という形の式が$81$個グレブナー基底に現れることになる． よってMacaulay2を使ってナンプレの答えを求めることができる．実際にこの例のコードを載せておくので，コピー＆ペーストで確かめてみてほしい．なお，グレブナー基底はかなり計算がかかる（ほとんど終わらない）ので初期状態が少ないとだいたい解けなくなる．実用的ではないが，色々な方法で問題を解くのは数学の醍醐味のひとつである．

8. 方程式に翻訳するという考え方

ここまで，ナンプレを多項式の連立方程式に翻訳する話を見た． このように，何かの対象を方程式で表すことは，実は高校数学でもすでに行っている．

たとえば，高校数学では軌跡の方程式を学ぶ． 円や直線などの図形を，点の集まりとして見るだけでなく， \[ x^2+y^2=1 \] のような方程式で表すのである． これは，図形を「式」に翻訳していると考えることができる．

図形を方程式に翻訳すると，視覚的な情報に頼らずに扱うことができる． 図を描かなくても計算できるし，複雑な図形も式として扱える． さらに，4次元以上の図形のように目に見えない対象も，方程式を使えば考えることができる．

ナンプレの場合も同じである． そのままでは，ナンプレは数字を書き込むパズルである． しかし，各マスを変数にし，ルールを多項式で表すと， \[ \text{ナンプレ} \quad\longrightarrow\quad \text{多項式の連立方程式} \] に翻訳できる．

この考え方は，情報科学やプログラミングでも重要である． 現実の問題をそのままコンピュータに渡すことはできない． まず，数学的・論理的な形に翻訳し，計算できる形にする必要がある． 今回の講義で見たグレブナー基底は，その一例である．

9. まとめ：概念の拡張と式への翻訳

今回の講義では，小学校で学ぶ自然数の割り算から出発した． 自然数の割り算では \[ a=qb+r,\qquad 0\leq r\lt b \] という形で，商と余りを定義した． 次に，この考え方を1変数多項式の割り算に拡張し，さらに辞書式順序を使って多変数多項式の割り算へ拡張した． また，複数の多項式で割ることを考えると，割る順番によって余りが変わるという問題が現れた． この問題を解決するための「良い割る多項式の集まり」がグレブナー基底である．

ここで大切なのは，単に新しい計算方法を覚えることではない． 自然数の割り算という身近な概念を定義し直し，それを多項式へ，さらに複数の多項式へと拡張していく． このように，既に知っている概念をより広い世界へ広げることは，大学数学の基本的な考え方の一つである．

さらに，ナンプレのようなパズルも，多項式の連立方程式に翻訳することで，グレブナー基底という数学の道具を使えるようになる． 高校数学で図形を軌跡の方程式として表すのと同じように，目に見える対象や具体的なルールを式に翻訳すると，計算やアルゴリズムの対象として扱うことができる．

• 自然数の割り算を定義し直す．
• その定義を多項式の割り算へ拡張する．
• 複数の多項式で割るときの問題から，グレブナー基底が現れる．
• 方程式に翻訳すると，図形やナンプレのような問題にもグレブナー基底を使える．

公式を覚えて計算するだけでなく，対象を定義し，概念を拡張し，現象を数学の言葉に翻訳する． これが，今回見てきた大学数学の考え方である．