3.1：イントロダクション
定義 3.1
$X$を空でない集合とする．$X$上の（二項）演算とは写像$f:X \times X \to X$のことをいう．つまり，演算とは，2つの要素から（同じ集合に属する）新しい要素を生み出す操作のことである．演算は$\circ, + ,*, \ldots$などを使い，$\circ(a,b)$の代わりに$a \circ b$と書くことが多い．こうするとこれまで知っている演算の形と思えるだろう．
例えば，整数の足し算や引き算，掛け算などは$\mathbb{Z}$上の演算である．演算といえば，こういった数に関する操作という認識があると思うが，どんな集合でも演算というものは考えられる．
例 3.2
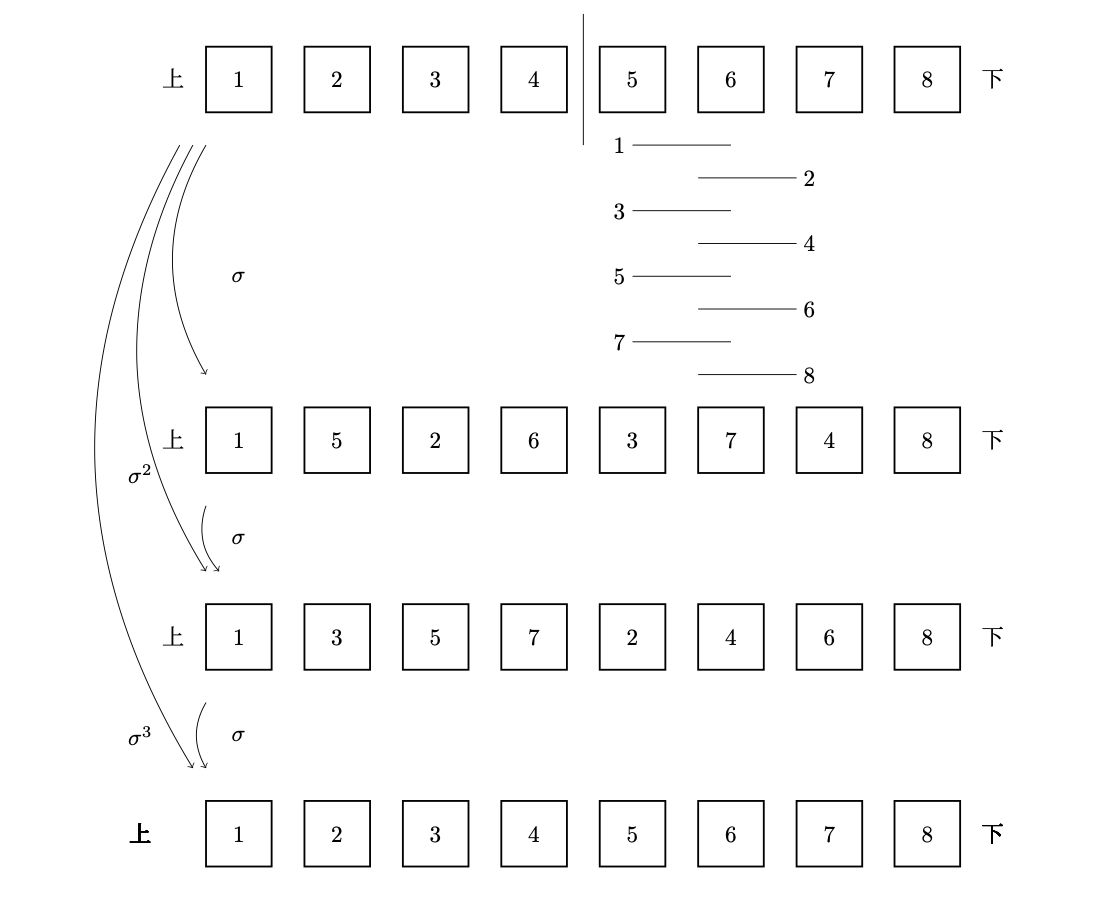
$1$から$8$の数字が書かれたカードの山を準備し，この山を切る（混ぜる）ことを考える．例えば，下図のように，上下に半分に分け，上の山のそれぞれのカードの間に下の山のカードが1枚ずつ入るように切る．
カードの切り方全体の集合を$X$とする．
このとき，$X$上の演算を次のように定義する．カードの切り方$\sigma_1,\sigma_2 \in X$に対し，$\sigma_1 \circ \sigma_2$を$\sigma_2$で切った後に，$\sigma_1$で切る操作として定義すると，この一連の流れももちろんカードの切り方の1つなので$\sigma_1 \circ \sigma_2 \in X$であり，$\circ$は$X$上の演算となる．
集合$X$とその集合上の演算$\circ$の対$(X,\circ)$を代数系という．
様々な操作は代数系を使って数学的に表現できる．
ここではこの代数系の最も基本となる群というものを考える．この群を考えることで様々な現象を群の性質を通して理解することができる．
例 3.3(例3.2の続き)
カードの山を何度か同じ切り方をしていくと，必ずもとのカードの山の状態に戻るという事実がある．例えば，例3.2で考えた切り方$\sigma$を3回すれば上図のように元に戻る．これは$\sigma^3=1$を意味している．ここで$1$は何もしないという切り方である．したがって上の事実はどんな切り方$\delta \in X$に対してもある自然数$n$で$\delta^n =1$となるものが存在することを意味している．これはカードの切り方の集合が有限群という代数構造を持つことから従う．
実はオイラーの定理も同様に証明できる．つまり，群を考えることで，一見全く違う集合の性質を統一的に証明することができる．このことを念頭に置いて群を学習していく．