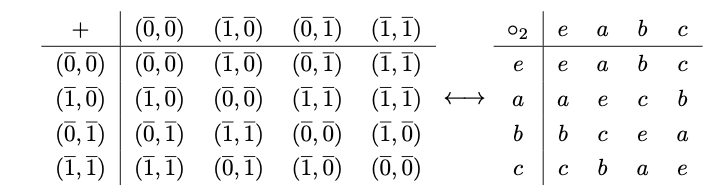3.6：直積群
2つの群から新たに群を構成することができる． $(G_1,\circ_1)$と$(G_2,\circ_2)$を単位元をそれぞれ$e_1$と$e_2$とする群とする． 今，直積$G_1 \times G_2$上の演算$\circ$を以下で定義する． \[ \circ : (G_1 \times G_2) \times (G_1 \times G_2) \to G_1 \times G_2; ((a_1,b_1),(a_2,b_2)) \mapsto (a_1 \circ_1 a_2, b_1 \circ_2 b_2). \]命題 3.26
$(G_1 \times G_2, \circ)$は単位元を$(e_1,e_2)$とする群である．
証明
演習問題とする．
例 3.27
直積群$\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$を考える．ただし，演算の記号として$+$を使う．これは以下の乗法表で定義される群である．
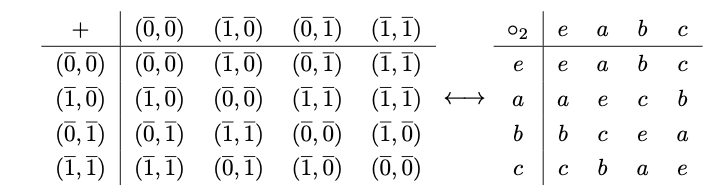今，$(\overline{0},\overline{0})=e, (\overline{1},\overline{0})=a,(\overline{0},\overline{1})=b,(\overline{1},\overline{1})=c$とすると，$\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$は例3.15で考えた$(G,\circ_2)$に他ならない．
一方で，同様に乗法表を比べることで$(G,\circ_1)$は$\mathbb{Z}/ 4\mathbb{Z}$と同一視することができる．したがって，例3.15で説明していたことは，$\mathbb{Z}/4\mathbb{Z}$と$\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$が「本質的には」違う有限群であるということである．しかし，実は$\mathbb{Z}/6\mathbb{Z}$と$\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z}$は「本質的には」同じ有限群である．つまり，この2つの群の乗法表は同じ形をしている．より詳しい説明は後の章で行う．