5.1：準同型写像
一般に，2つの集合を比べるとき，その集合間の写像を考えることは基本である．しかし，単なる集合ではなく，群として比べたいときは，特別な写像を考える．定義 5.1
$(G_1, \circ_1),(G_2,\circ_2)$を群とする．写像$f : G_1 \to G_2$が（群）準同型写像 (homomorphism)であるとは，任意の$a,b \in G_1$に対し，
\[
f(a \circ_1 b)=f(a) \circ_2 f(b)
\]
を満たすときにいう．
乗法表で見ると，準同型写像というのは，写像で移る前の演算の対応と，移った先の演算の結果が一致しているということである．
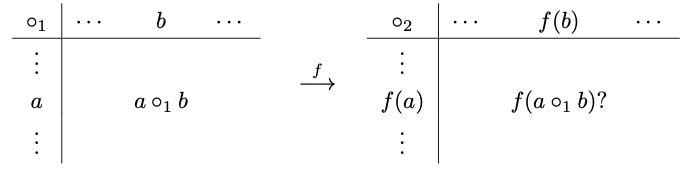
命題 5.2
$G_1,G_2$を群とし，$f:G_1 \to G_2$を準同型写像とする．このとき，以下が成り立つ．
証明
$e_1 \circ_1 e_1=e_1$より，
\[
f(e_1)=f(e_1 \circ_1 e_1)=f(e_1) \circ_2 f(e_1)
\]
である．したがって$G_2$における単位元の一意性から$f(e_1)=e_2$となる．
(2) 示すべきことは$f(a)$の逆元が$f(a^{-1})$となることである． これは \begin{align*} f(a) \circ_2 f(a^{-1})=f(a \circ_1 a^{-1})=f(e_1)=e_2\\ f(a^{-1}) \circ_2 f(a)=f(a^{-1} \circ_1 a)=f(e_1)=e_2 \end{align*} から従う．
それでは準同型写像の例をいくつか見ていこう．
(2) 示すべきことは$f(a)$の逆元が$f(a^{-1})$となることである． これは \begin{align*} f(a) \circ_2 f(a^{-1})=f(a \circ_1 a^{-1})=f(e_1)=e_2\\ f(a^{-1}) \circ_2 f(a)=f(a^{-1} \circ_1 a)=f(e_1)=e_2 \end{align*} から従う．
例 5.3
(1) 群$G_1,G_2$に対し，$f :G_1 \to G_2$を$g \mapsto e_2$で定義する．つまり，全ての元が$G_2$の単位元に移るような写像を考える．すると任意の$a,b \in G_1$に対し，
\[
f(a \circ_1 b)=e_2=e_2 \circ_2 e_2 =f(a) \circ_2 f(b)
\]
が成り立つので，$f$は準同型写像である．これを自明な準同型写像という．
(2) 2倍写像$f: \mathbb{Z} \to \mathbb{Z},x \mapsto 2x$を考えよう．任意の$x,y \in \mathbb{Z}$に対し， \[ f(x+y)=2(x+y)=2x+2y=f(x)+f(y) \] であるので，$f$は準同型写像である．
(3) 写像$f : \mathbb{Z} \to \mathbb{Z}, x \mapsto x+2$を考える． このとき， \[ f(1+1)=f(2)=2+2=4 \neq (1+2)+(1+2) =f(1)+f(1) \] より，任意の$x,y \in \mathbb{Z}$に対し，$f(x+y)=f(x)+f(y)$が成り立つとは限らない．よって$f$は準同型写像ではない．
(4) 正則な$2$次正方行列全体の集合${\rm GL}_2(\mathbb{R})$は行列の積に関して群であった．また$(\mathbb{R}^{\times},\cdot)$も群であった． 写像$f : {\rm GL}_2(\mathbb{R}) \to \mathbb{R}^{\times}$を$A \mapsto \det A$で定義する．ここで$\det A$は$A$の行列式を表す． このとき，任意の$A,B \in {\rm GL}_2(\mathbb{R})$に対し，$\det AB=\det A \cdot \det B$であったことを思い出すと， \[ f(AB)=\det AB=\det A \cdot \det B=f(A) \cdot f(B) \] が成り立つので，$f$は準同型写像である．
写像$f: G_1 \to G_2$があったとき，元$x \in G_1$に対し，$f(x) \in G_2$を$x$の$f$に関する像 (image)と呼ぶ．また像全体の集合
\[ {\rm Im}(f):=\{ f(x) \in G_2 : x \in G_1\}\]
を$f$の像と呼ぶ．
一般に$G_1,G_2$が群であったとしても${\rm Im}(f)$が群になるとは限らない．しかし，$f$が準同型写像であればいつでも${\rm Im}(f)$は群となる．
(2) 2倍写像$f: \mathbb{Z} \to \mathbb{Z},x \mapsto 2x$を考えよう．任意の$x,y \in \mathbb{Z}$に対し， \[ f(x+y)=2(x+y)=2x+2y=f(x)+f(y) \] であるので，$f$は準同型写像である．
(3) 写像$f : \mathbb{Z} \to \mathbb{Z}, x \mapsto x+2$を考える． このとき， \[ f(1+1)=f(2)=2+2=4 \neq (1+2)+(1+2) =f(1)+f(1) \] より，任意の$x,y \in \mathbb{Z}$に対し，$f(x+y)=f(x)+f(y)$が成り立つとは限らない．よって$f$は準同型写像ではない．
(4) 正則な$2$次正方行列全体の集合${\rm GL}_2(\mathbb{R})$は行列の積に関して群であった．また$(\mathbb{R}^{\times},\cdot)$も群であった． 写像$f : {\rm GL}_2(\mathbb{R}) \to \mathbb{R}^{\times}$を$A \mapsto \det A$で定義する．ここで$\det A$は$A$の行列式を表す． このとき，任意の$A,B \in {\rm GL}_2(\mathbb{R})$に対し，$\det AB=\det A \cdot \det B$であったことを思い出すと， \[ f(AB)=\det AB=\det A \cdot \det B=f(A) \cdot f(B) \] が成り立つので，$f$は準同型写像である．
命題 5.4
$G_1,G_2$を群とし，$f:G_1 \to G_2$を準同型写像とする．このとき${\rm Im}(f)$は$G_2$の部分群である．
証明
任意の$f(x), f(y) \in {\rm Im}(f)$ $(x,y \in G_1)$をとる．
このとき，
\[
f(x) \circ_2 f(y)^{-1}=f(x) \circ_2 f(y^{-1})=f(x \circ y^{-1}) \in {\rm Im}(f)
\]
であるので，${\rm Im}(f)$は$G_2$の部分群である．
したがって$f:G_1 \to G_2$が準同型写像であれば，${\rm Im}(f)$は$G_1$の群構造を「ある程度」引き継いだ$G_2$の部分群であることがわかる．
特に，${\rm Im}(f)$はもとの群$G_1$の性質を引き継ぐことが多い．例えば，以下のような性質がある．
命題 5.5
$G_1,G_2$を群とし，$f : G_1 \to G_2$を準同型写像とする．このとき，$G_1$が巡回群であれば，${\rm Im}(f)$も巡回群である．
証明
任意の$x \in G_1$と整数$n$に対して，$f$の準同型性から
\[
f(x^n)=(f(x))^n
\]
となることがわかる．
今，$a \in G_1$を使って
$G_1=\langle a \rangle$と書けるとする．
すると，
\[ {\rm Im}(f)=\{ f(x) : x \in G_1\}=\{f(a^n) : n \in \mathbb{Z}\}=\{(f(a))^n : n \in \mathbb{Z}\}=\langle f(a) \rangle
\]
となり，${\rm Im}(f)$が巡回群であることがわかった．
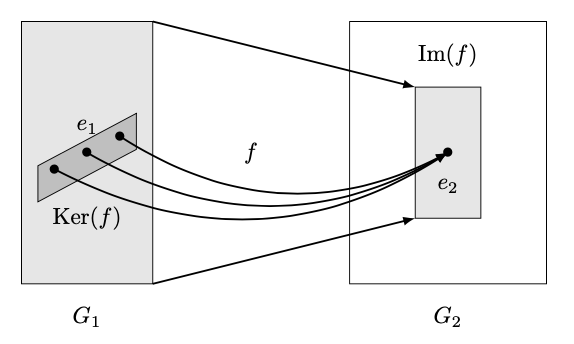
準同型写像$f: G_1 \to G_2$に対して，${\rm Im}(f)$は$G_1$の群構造を「ある程度」引き継ぐといったが，これは一部の群構造が「潰れる」ときがあるのでこのように表現した．実際，自明な準同型写像を考えると，全てが単位元に飛ぶので群構造がほとんど「潰れる」のがわかるだろう．この「潰れる」元全体の集合を考える．
定義 5.6
$G_1,G_2$を群とし，$f : G_1 \to G_2$を準同型写像とする．このとき，集合
\[
{\rm Ker}(f):=\{ x \in G_1 : f(x)=e_2\} \subset G_1
\]
を$f$の核 (kernel)という．
下図のように，${\rm Ker}(f)$とは単位元1点に圧縮される集合のことである．
命題 5.7
$G_1,G_2$を群とし，$f:G_1 \to G_2$を準同型写像とする．このとき${\rm Ker}(f)$は$G_1$の部分群である．
証明
任意の$x,y \in {\rm Ker}(f)$をとる．このとき$f(x) =f(y)=e_2$である．
また$f(y^{-1})=f(y)^{-1}=e_2^{-1}=e_2$である．
すると
\[ f(x \circ_1 y^{-1})=f(x) \circ_2 f(y^{-1})=e_2 \circ_2 e_2=e_2\]
であるので，$x \circ_1 y^{-1} \in {\rm Ker}(f)$が従う．よって${\rm Ker}(f)$は$G_1$の部分群である．
$f$が準同型写像の場合，${\rm Ker}(f)$を調べることで$f$が単射かどうか判定できる．
命題 5.8
準同型写像$f: G_1 \to G_2$が単射である必要十分条件は${\rm Ker}(f)=\{e_1\}$である．
証明
（$\Rightarrow$）$x \in {\rm Ker}(f)$とすると，
\[
f(x)=e_2=f(e_1)
\]
である．$f$が単射であるので，$x=e_1$が成り立ち，${\rm Ker}(f)=\{e_1\}$が従う．
（$\Leftarrow$）任意の$x,y \in G_1$で$f(x)=f(y)$を満たすものをとる．このとき，$f$の準同型性より \[ e_2=f(x) \circ_2 f(x^{-1}) = f(y) \circ_2 f(x^{-1})=f(y \circ_1 x^{-1}) \]である． よって$y \circ_1 x^{-1} \in {\rm Ker}(f)=\{e_1\}$が成り立つので，$y \circ_1 x^{-1}=e_1$となり，$y=x$を得る．よって$f$は単射である．
この命題から，${\rm Im}(f)$が潰れないことと$f$が単射であることが同値であることがわかる．
（$\Leftarrow$）任意の$x,y \in G_1$で$f(x)=f(y)$を満たすものをとる．このとき，$f$の準同型性より \[ e_2=f(x) \circ_2 f(x^{-1}) = f(y) \circ_2 f(x^{-1})=f(y \circ_1 x^{-1}) \]である． よって$y \circ_1 x^{-1} \in {\rm Ker}(f)=\{e_1\}$が成り立つので，$y \circ_1 x^{-1}=e_1$となり，$y=x$を得る．よって$f$は単射である．