13回目:無限集合
13.1 無限集合の濃度
$2$つの有限集合の濃度の大小関係は,それぞれの要素の個数を比較すればできたが,無限集合の場合はそもそも要素が無限個あるので,要素の個数では比較できない.しかし,有限集合の場合,写像を使って比較できたことを思い出そう(12.2節).その性質をそのまま無限集合での濃度の比較で使う.定義
有限集合とは限らない集合$X$と$Y$に対し,
一般に,集合$X,Y,Z$に対し,
\[
|X| \approx |Y| \land |Y| \approx |Z| \Rightarrow |X| \approx |Z|
\]
\[
|X| \precsim |Y| \land |Y| \precsim |Z| \Rightarrow |X| \precsim |Z|
\]
が成り立つ(このような性質を推移律という).
これは次の合成写像の性質から従う(証明略).
- 全単射$f: X \to Y$が存在するとき,$X$と$Y$は濃度が等しいといい,$|X| \approx |Y|$と書く.
- 単射$f :X \to Y$が存在するとき,$X$の濃度は$Y$の濃度以下であるといい,$|X| \precsim |Y|$と書く. 特に,$|X| \not\approx |Y|$のときは,$|X| \prec |Y|$と書き,$X$の濃度は$Y$の濃度より小さいという.
命題 13.1
集合$X,Y,Z$と写像$f : X \to Y$と$g: Y \to Z$に関して,$f,g$がともに単射(全射,全単射)ならば$g \circ f$も単射(全射,全単射)である.
また集合$X,Y$が$X \subset Y$を満たしていれば,
$|X| \precsim |Y|$
となる.これは写像$\iota_{X,Y}: X \to Y, a \mapsto a$が明らかに単射となるからである.この写像$\iota_{X,Y}$は$X$から$Y$への包含写像と呼ばれる.
13.2 可算集合
自然数全体の無限集合$\mathbb{N}=\{1,2,3,\ldots\}$の濃度を$\aleph_0$と書く($\aleph$はヘブライ文字の最初の文字であり,アレフと呼ぶ ). 実は$\aleph_0$は無限集合の中で最も小さい濃度である.定義
濃度が$\aleph_0$と等しい集合を可算集合 (countable set) と呼ぶ.つまり,可算集合は最も濃度が小さい無限集合のことである.可算集合でない無限集合を非可算集合 (uncountable set) と呼ぶ.つまり,非可算集合は$\mathbb{N}$より濃度が大きい集合のことである.
例えば,正の偶数の集合$E=\{2,4,6,\cdots\}$を考える.$f(n)=2n$で表される写像$f: \mathbb{N} \to E$は全単射である.したがって,$E$は$\mathbb{N}$と同じ濃度を持つので,
$
|E| \approx \aleph_0
\nonumber
$
となる.
集合$X$が可算集合であれば全単射$f:\mathbb{N} \to X$が存在する.このとき,各自然数$i$に対し$f(i)=x_i$とすると,$X=\{x_1,x_2,x_3 \ldots\}$のように$X$の要素を$1$番目, $2$番目, $\ldots$と並べることができる.このように要素を順番付けられる無限集合が可算集合である.英語のcountableの意味通りである.
非可算集合の例は次の命題を使うことで簡単に作ることができる.
命題 13.2
$X$を空集合でない集合とする.このとき次が成り立つ.
\[
|X| \prec |2^X|.
\]
証明
写像$f : X \to 2^X$を$x \mapsto \{x\}$で定義すると,これは明らかに単射である(理由を説明できるようにしよう).よって$|X| \precsim |2^X|$である.
背理法を使って$X$と$2^X$の間に全単射が存在しないことを証明する.
全単射写像$f : X \to 2^X$が存在したと仮定する.
このとき,$X$の部分集合$A$を
\[
A=\{ a \in X: a \notin f(a)\}
\]
で定義する.
特に,$A \in 2^X$であることに注意する.$f$は全射なので,$f(a)=A$となる$X$の要素$a \in X$が存在する.
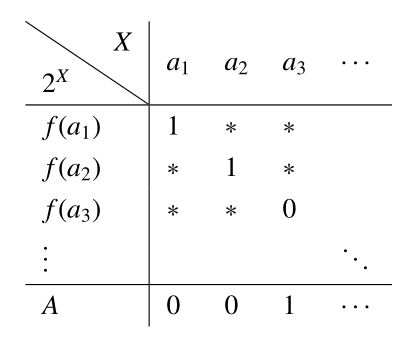
上記のような$A=\{a : a \notin f(a)\}$という集合を使った証明方法を対角線論法という.
なぜこのような呼び方をするかというと,
わかりやすいように,$X$を可算集合$X=\{a_1,a_2,a_3,\ldots\}$とし,$a_1 \notin f(a_1), a_2 \notin f(a_2), a_3 \in f(a_3)$とする.
下の図のように,$a \notin f(b)$なら$1$,$a \in f(b)$なら$0$を入れていく.
- $a \in A$のとき,$A$の定義より,$a \notin f(a)$である.しかし$f(a)=A$より,$a \notin A$となって矛盾.
- $a \notin A$のとき,$A$の定義より,$a \in f(a)$である.しかし$f(a)=A$より,$a \in A$となって矛盾.