12回目:濃度
12.1 有限集合の濃度
定義
有限集合$A$がちょうど$n$個の要素を持つとき,記号
\[
|A| = n
\]
で表すこととする.これを集合$A$の濃度 (cardinality) という.
$B$が$A$の部分集合であればいつでも$|B| \leq |A|$である.
有限集合$A, B$に対して次の式が成り立つ. \[ |A\cup B| = |A| + |B| - |A \cap B| \] \[ |A \cup B \cup C| = |A| + |B| + |C| - |B \cap C| - |A \cap B| - |A \cap C| + |A \cap B \cap C| \] 一般に$n$個の有限集合$A_1, A_2, A_3, \ldots, A_n$の和集合の要素の個数について次の式が成り立つ. \begin{eqnarray} |A_1 \cup A_2 \cup \cdots \cup A_n| &=& \sum^n_{i=1}|A_i|-\sum_{1 \leq i \lt j \leq n}|A_i\cap A_j| + \sum_{1 \leq i \lt j \lt k \leq n}|A_i\cap A_j \cap A_k| - \cdots \nonumber\\ & & +(-1)^{n-1}|A_1 \cap A_2 \cap \cdots \cap A_n| \nonumber \end{eqnarray} この公式を包除原理という.
12.2 写像による濃度の比較
2つの有限集合$X,Y$の濃度の比較は$X$から$Y$へのある写像の存在によって可能である.- $|X| \leq |Y| \Leftrightarrow$ 単射$f :X \to Y$が存在する.
- $|X| \geq |Y| \Leftrightarrow$ 全射$f :X \to Y$が存在する.
- $|X|=|Y| \Leftrightarrow$ 全単射$f :X \to Y$が存在する.
証明
$|X|=n, |Y|=m$とし,$X=\{a_1,a_2,\ldots,a_n\}, Y=\{b_1,b_2,\ldots,b_m\}$とおく.
それぞれ$\Rightarrow$を証明する.
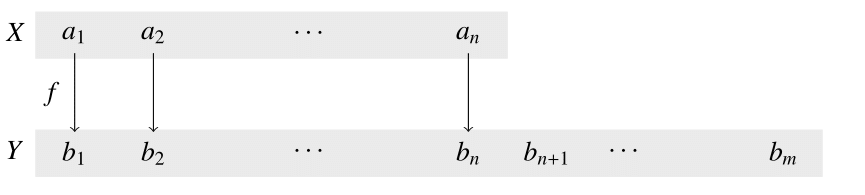
(1) $n \leq m$なので,各$1 \leq i \leq n$に対し,$f(a_i)=b_i$となる写像$f: X \to Y$が定義でき,これは単射である.
 (2) $m \leq n$なので,各$1 \leq i \leq n$に対し,
\[
f(a_i)= \begin{cases}
b_i & (1 \leq i \leq m-1)\\
b_m & (m \leq i \leq n)
\end{cases}
\]
となる$f: X \to Y$が定義でき,これは全射である.
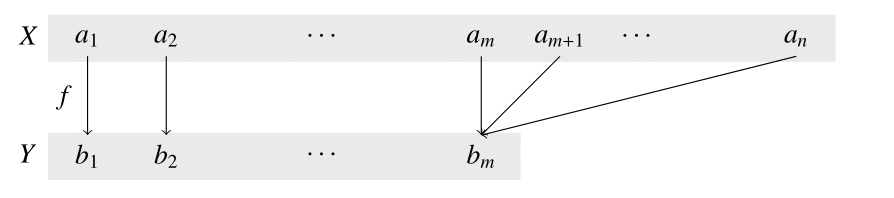
(2) $m \leq n$なので,各$1 \leq i \leq n$に対し,
\[
f(a_i)= \begin{cases}
b_i & (1 \leq i \leq m-1)\\
b_m & (m \leq i \leq n)
\end{cases}
\]
となる$f: X \to Y$が定義でき,これは全射である.
 (3) $n=m$なので,(1)と(2)で定義した写像が両方定義でき,特に,この2つの写像は一致する.したがってこの写像は全単射である.
(3) $n=m$なので,(1)と(2)で定義した写像が両方定義でき,特に,この2つの写像は一致する.したがってこの写像は全単射である.
次に(1)と(2)の$\Leftarrow$をそれぞれ証明する ((3)は(1)と(2)から従う).
(1) $f : X \to Y$が単射であるので,$|X|=|{\rm Im}(f)|$が成り立つ.また${\rm Im}(f) \subset Y$から$|{\rm Im}(f)| \leq |Y|$となり,$|X| \leq |Y|$が成り立つ.
(2) $f : X \to Y$が全射であるので,${\rm Im}(f)=Y$,特に,$|{\rm Im}(f)|=|Y|$が成り立つ.一般に,$|X| \geq |{\rm Im}(f)|$なので,$|X| \geq |Y|$が従う.
(1) $n \leq m$なので,各$1 \leq i \leq n$に対し,$f(a_i)=b_i$となる写像$f: X \to Y$が定義でき,これは単射である.


次に(1)と(2)の$\Leftarrow$をそれぞれ証明する ((3)は(1)と(2)から従う).
(1) $f : X \to Y$が単射であるので,$|X|=|{\rm Im}(f)|$が成り立つ.また${\rm Im}(f) \subset Y$から$|{\rm Im}(f)| \leq |Y|$となり,$|X| \leq |Y|$が成り立つ.
(2) $f : X \to Y$が全射であるので,${\rm Im}(f)=Y$,特に,$|{\rm Im}(f)|=|Y|$が成り立つ.一般に,$|X| \geq |{\rm Im}(f)|$なので,$|X| \geq |Y|$が従う.