3回目:二項関係
3.1 二項関係
東邦大学の学生の集合$X$を,仮に \[ X=\{\mbox{フェルマー,オイラー,ガウス,セール,ヒルベルト,エルデシュ}\} \] とし,東邦大学の学部の集合を \[Y=\{\mbox{医,薬,理,看護,健康科学}\}\] とする.集合$X$と集合$Y$を個別に考えると,これらはただの独立した集合であるが,「学生」と「その学生が所属する学部」を考えると,2つの集合の要素の間に「関係」が現れる.例えば,「フェルマーは医」,「オイラーは看護」,「ガウスは理」,「セールは健康科学」,「ヒルベルトは薬」,「エルデシュは理」としよう.この「関係」というものを数学的に定義するにはどうすればいいか.上の「関係」は結局, $X$の要素(学生)$x$と$Y$の要素(学部)$y$の組の集まりである.これは順序対$(x,y)$を使って表すのがよさそうである.実際,直積集合$X \times Y$の部分集合$R$を \[ R=\left\{\mbox{(フェルマー, 医)},\mbox{(オイラー, 看護)}, \mbox{(ガウス, 理)},\mbox{(セール, 健康科学)},\mbox{(ヒルベルト, 薬)},\mbox{(エルデシュ, 理)} \right\} \] とすると,この集合$R$は上の「関係」を完全に表していることが分かるであろう.これを踏まえて2つの集合の「関係」を定義する.ここで,$X=Y$とし,次の$X$上の関係を考える: \[ {\rm Id}_{X}=\{ (x,x) : x \in X\}=\{ (x_1,x_2) \in X \times X : x_1=x_2\}. \] この関係を$X$の恒等関係 (identity relation)という.
3.2 矢線図と有向グラフ
有限集合$X$と$Y$が有限集合のとき,$X$から$Y$への関係は矢線図 (arrow diagram)を用いて表現することができる.例えば,前ページの「学生」と「学部」の関係の矢線図は以下の左図のようになる.また,集合$X$上の関係は矢線図の他に有向グラフ (directed graphまたはdigraph)を用いて表現することもできる.例えば,例3.2の$X$上の関係$R$は以下の右図で表現される.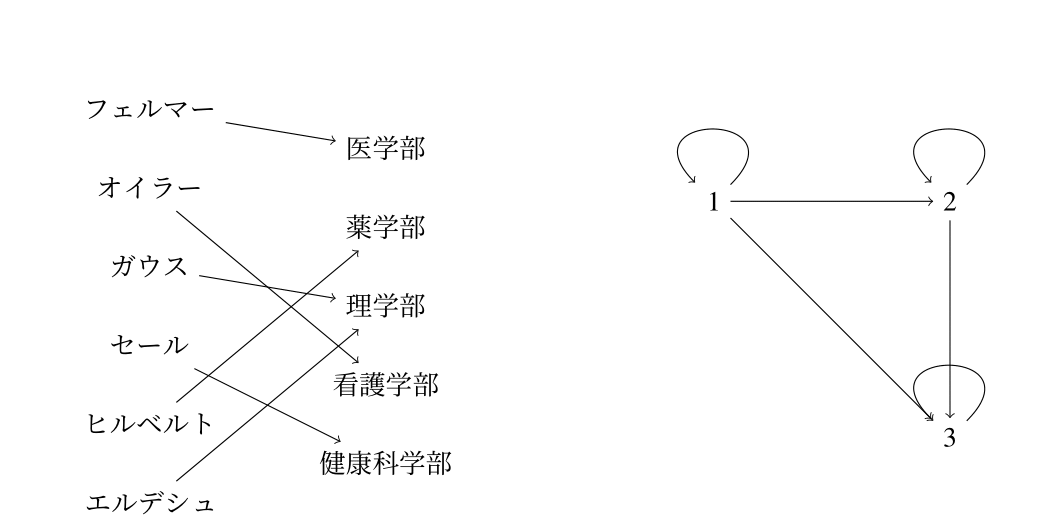
3.3 二項関係の演算
2つの$X$から$Y$への関係$R$と$S$を考える.このとき,$R$と$S$は$X \times Y$の部分集合であるので,その合併$R \cup S$,共通部分$R \cap S$,差$R \setminus S$は再び$X \times Y$の部分集合となるので,これらも$X$から$Y$への関係である.つまり,$X$から$Y$への関係は,これら集合の演算で閉じていることがわかる.- $ R=\{ (1,a), (2,b), (2,c),(3,b)\} $ は「学生」と「その学生が受講している科目」を表す関係,
- $ S=\{ (1,a), (1,b), (2,b),(3,c)\} $ は「学生」と「その学生が興味を持っている科目」を表す関係.
- $ R \cup S=\{(1,a),(1,b),(2,b), (2,c),(3,b),(3,c)\} $ は「学生」と「その学生が受講している,または興味を持っている科目」 を表す関係,
- $ R \cap S = \{ (1,a), (2,b)\} $ は「学生」と「その学生が興味を持って受講している科目」を表す関係,
- $ R \setminus S = \{ (2,c), (3,b)\} $ は「学生」と「その学生が受講しているが興味のない科目」を表す関係
3.4 逆関係
$R$を$X$から$Y$への関係,つまり$R \subset X \times Y$とする.このとき,$R$の逆関係 (inverse relation) $R^{-1}$は,$\{(y,x) \in Y \times X : (x,y) \in R\}$で与えられる$Y$から$X$への関係である.定義から$xRy \iff yR^{-1}x$が従う.- $ R^{-1}=\{ (a,1), (b,2), (c,2),(b,3)\} $ は「科目」と「その科目を受講している学生」を表す関係,
- $ S^{-1}=\{ (a,1), (b,1), (b,2),(c,3)\} $ は「科目」と「その科目に興味を持っている学生」を表す関係
$(R^{-1})^{-1}=R$
$R \subset S$ならば$R^{-1} \subset S^{-1}$
$(R \cup S)^{-1}=R^{-1} \cup S^{-1}$
$(R \cap S)^{-1}=R^{-1} \cap S^{-1}$
まず$(R \cup S)^{-1} \subset R^{-1} \cup S^{-1}$を示す.ここで$(R \cup S)^{-1}$と$R^{-1} \cup S^{-1}$は$Y$から$X$への関係であることに注意する.任意の$(y,x) \in (R \cup S)^{-1} $をとると,このとき,逆関係の定義から$(x,y) \in R \cup S$である.つまり$(x,y) \in R$または$(x,y) \in S$である.これは,再び逆関係の定義から,$(y,x) \in R^{-1}$または$(y,x) \in S^{-1}$を意味するので,$(y,x) \in R^{-1} \cup S^{-1}$が従う.よって$(R \cup S)^{-1} \subset R^{-1} \cup S^{-1}$となる.
次に,$R^{-1} \cup S^{-1} \subset (R \cup S)^{-1}$を示す.任意の$(y,x) \in R^{-1} \cup S^{-1}$をとると,これは$(y,x) \in R^{-1}$または$(y,x) \in S^{-1}$を意味する.逆関係の定義より,$(x,y) \in R$または$(x,y) \in S$が従い,つまり$(x,y) \in R \cup S$となる.このとき,再び逆関係の定義から,$(y,x) \in (R \cup S)^{-1}$が従う.よって$R^{-1} \cup S^{-1} \subset (R \cup S)^{-1}$となる.
以上から$(R \cup S)^{-1} = R^{-1} \cup S^{-1}$が証明できた.
3.5 合成関係
集合$X$から$Y$への二項関係$R$と集合$Y$から$Z$への関係$S$を考える.このとき,$X$から$Z$への関係$S \circ R$(これで一つの関係を表す)を \[ S \circ R = \{ (x,z) \in X \times Z : \mbox{ある$y\in Y$に対して$xRy$かつ$ySz$である} \} \] により定めることができる.すなわち, \[ S \circ R = \{ (x,z) \in X \times Z : \exists y \in Y ( (x,y) \in R \land (y,z) \in S) \} \] である.これを$R$と$S$の合成関係 (composite relation)という.$R$と$S$の順番を間違えないように注意!- $R=\{(1,a),(2,b),(2,c),(3,b),(3,c),(3,d)\}$を「学生」と「その学生が受講している科目」を表す関係,
- $S=\{(a, \alpha), (b, \beta), (b,\gamma), (c,\gamma), (d, \gamma) \}$を「科目」と「その科目を担当している先生」を表す関係
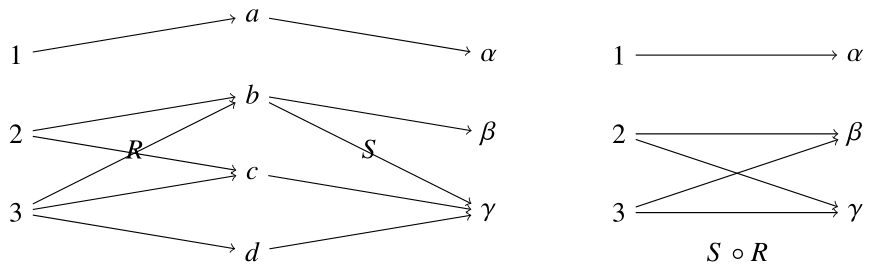
$(S \circ R)^{-1}=R^{-1} \circ S^{-1}$,
$T \circ (S \circ R)= (T \circ S) \circ R$(関係の合成に関する結合則),
$R \circ {\rm Id}_X=R$かつ${\rm Id}_Y \circ R=R$.
(1) $(z,x) \in Z \times X$とすると,このとき, \begin{align*} (z,x) \in (S \circ R)^{-1} &\iff (x,z) \in S \circ R & \mbox{(逆関係の定義)}\\ &\iff \exists y \in Y ( (x,y) \in R \land (y,z) \in S) & \mbox{(合成関係の定義)}\\ &\iff \exists y \in Y ( (y,x) \in R^{-1} \land (z,y) \in S^{-1}) & \mbox{(逆関係の定義)}\\ &\iff \exists y \in Y ( (z,y) \in S^{-1} \land (y,x) \in R^{-1}) & \mbox{(論理の交換律)}\\ &\iff (z,x) \in R^{-1} \circ S^{-1} & \mbox{(合成関係の定義)} \end{align*} よって$(S \circ R)^{-1}=R^{-1} \circ S^{-1}$である.
(2) 次の事実に注意する. \begin{equation} \exists x P(x) \land Q \iff \exists x ( P(x) \land Q) \tag{*} \end{equation} \begin{equation} \exists x \exists y P(x,y) \iff \exists y \exists x P(x,y) \tag{**} \end{equation} $(x,w) \in X \times W$とすると, このとき, \begin{align*} (x,w) \in T \circ (S \circ R) &\iff \exists z \in Z ( \underline{(x,z) \in S \circ R} \land (z,w) \in T) & \mbox{(合成関係の定義)}\\ &\iff \exists z \in Z ( \underline{(\exists y \in Y((x,y) \in R \land (y,z) \in S ))} \land \underline{(z,w) \in T}) & \mbox{(合成関係の定義)}\\ &\iff \exists z \in Z ( \exists y \in Y(\underline{((x,y) \in R \land (y,z) \in S ) \land (z,w) \in T})) & \mbox{(*)}\\ &\iff \underline{\exists z \in Z \, \exists y \in Y}((x,y) \in R \land (y,z) \in S \land (z,w) \in T) & \mbox{(論理の結合律)}\\ &\iff \exists y \in Y \, \underline{\exists z \in Z} ( \underline{(x,y) \in R} \land (y,z) \in S \land (z,w) \in T) & \mbox{(**)}\\ &\iff \exists y \in Y ((x,y) \in R \land \underline{\exists z \in Z( (y,z) \in S \land (z,w) \in T) })& \mbox{(*)}\\ &\iff \exists y \in Y ((x,y) \in R \land (y,w)\in T \circ S)& \mbox{(合成関係の定義)}\\ &\iff (x,w) \in (T \circ S) \circ R & \mbox{(合成関係の定義)} \end{align*} よって$T \circ (S \circ R)= (T \circ S) \circ R$である.
(3) $(x,y) \in X \circ Y$とすると,このとき, \begin{align*} (x,y) \in R \circ {\rm Id}_X & \iff \exists x' \in X ( (x,x') \in {\rm Id}_X \land (x',y) \in R) & \mbox{(合成関係の定義)}\\ &\iff \exists x' \in X (x=x' \land (x',y) \in R) & \mbox{(恒等関係の定義)}\\ &\iff (x,y) \in R \end{align*} よって$R \circ {\rm Id}_X=R$である.${\rm Id}_Y \circ R=R$も同様.