4回目:同値関係
直積集合$X \times Y$の部分集合のことを,$X$から$Y$への(二項)関係, 特に,$X=Y$のときは,$X$上の(二項)関係と呼んでいた. 本節では特別な$X$上の関係を考えることで,集合$X$における「等しい($=$)」という概念を拡張する.4.1 反射的な関係
定義 4.1
集合$X$上の関係$R$が反射的 (reflexive)であるとは,任意の$x \in X$に対して$(x,x) \in R$であるときにいう.つまり,
$R$が反射的である $\iff \forall x \in X ( (x,x) \in R) \iff {\rm Id}_X \subset R$
である.
ここで,${\rm Id}_X$は$X$の恒等関係である.
例 4.2
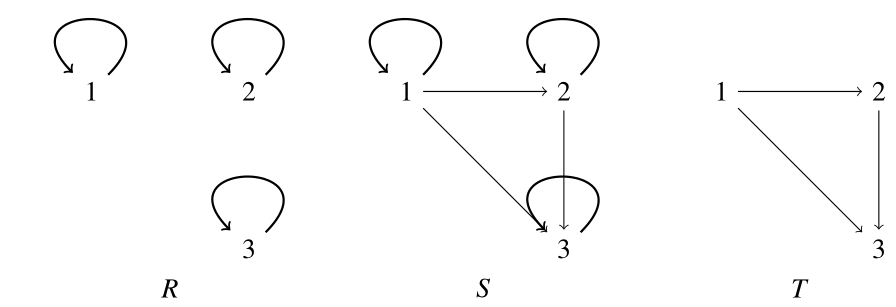
$X=\{1,2,3\}$とし,$X$上の関係
\begin{align*}
R&=\{(1,1), (2,2), (3,3)\} \\
S&=\{(1,1), (1,2), (1,3), (2,2), (2,3),(3,3)\}\\
T&=\{(1,2),(1,3),(2,3)\}
\end{align*}
を考える.$R,S,T$はそれぞれ,$=,\leq, \lt $という関係を表していることに注意する.
特に,$R$は$X$の恒等関係${\rm Id}_X$に他ならない.反射律の3つ目の同値条件を考えると,
${\rm Id}_X \subset {\rm Id_X}$なので,$R$は反射的である.また$R \subset S$なので,$S$も反射的である.
一般に,反射的な関係を部分集合に持つ関係は,再び反射的となる.
最後に$T$を考えると,$1 \in X$に対して,$(1,1) \notin T$なので,$T$は反射的ではない.
有向グラフで考えると,反射的な関係とは,全ての頂点にループ辺が存在する関係のことである.
4.2 対称的な関係
定義 4.3
集合$X$上の関係$R$が対称的 (symmetric)であるとは,任意の$a,b \in X$に対して$(a,b) \in R$ならばいつでも$(b,a) \in R$であるときにいう.つまり,
$R$が対称的である $\iff \forall a, b \in X ((a,b) \in R \rightarrow (b,a) \in R ) \iff R=R^{-1}$.
ここで,$R^{-1}$は$R$の逆関係である.
例 4.4
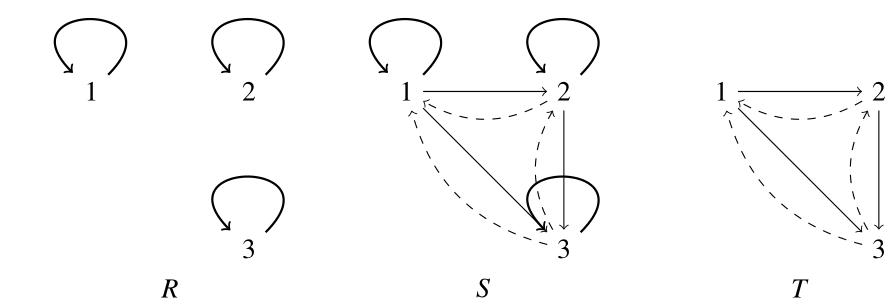
例4.2の集合$X$と$X$上の関係$R,S,T$を考える.任意の集合$A$に対して,$({\rm Id}_A)^{-1}={\rm Id}_A$であるので,$R$は対称的である.一方,$1,2 \in X$に対し,$(1,2) \in S$(同様に$(1,2) \in T$)であるが,$(2,1) \notin S$(同様に$(2,1) \notin T$)であるので,$S$および$T$は対称的ではない.
有向グラフで見ると,対称的な関係とは,ある頂点から頂点への矢印があれば,必ず逆方向の矢印も存在する関係である.ただし,ループ辺は自分自身が逆向きの矢印となる.
4.3 推移的な関係
定義 4.5
集合$X$上の関係$R$が推移的 (transitive)であるとは,任意の$a,b,c \in X$に対して,$(a,b) \in R$かつ$(b,c) \in R$ならばいつでも$(a,c) \in R$となるときをいう.つまり,
$R$が推移的である $\iff \forall a,b,c \in X ( (aRb \land bRc) \rightarrow aRc) \iff R \circ R \subset R$.
ここで,$R \circ R$は$R$と$R$の合成関係である.
例 4.6
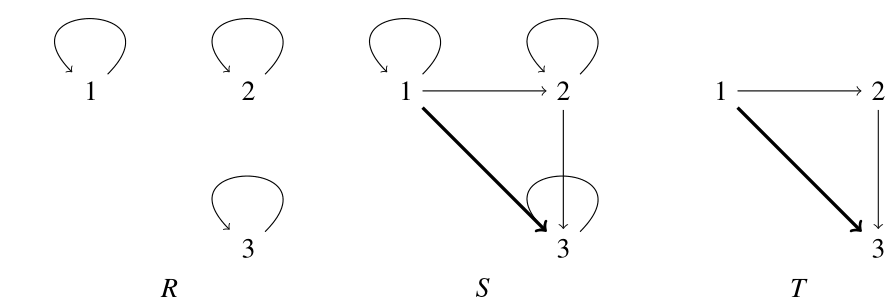
例4.2の集合$X$と$X$上の関係$R,S,T$を考える.任意の集合$A$に対して,${\rm Id}_A \circ {\rm Id}_A={\rm Id}_A \subset {\rm Id}_A$であるので,$R$は推移的である.一方,簡単な計算により,
$S \circ S=S$と$T \circ T=\{(1,3)\} \subset T$がわかるので,$S$も$T$も推移的となる.有向グラフで考えると,推移的な関係とは,ある2頂点が2つの矢印を通り辿り着けるなら,その2点間に近道となる矢印が必ずあるということである.
例 4.7
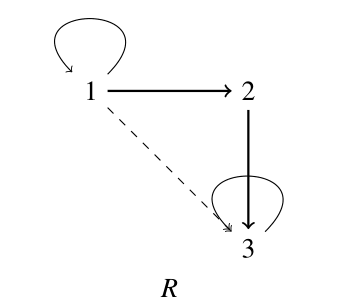
推移的でない二項関係の例も見ておこう.$X=\{1,2,3\}$とし,$X$上の二項関係を
\[
R=\{ (1,1), (1,2), (2,3),(3,3)\}
\]
とすると,$(1,2), (2,3) \in R$だが,$(1,3) \notin R$なので,$R$は推移的ではない.
特に,
\[
R \circ R=\{ (1,1), (1,2), (1,3), (2,3), (3,3)\}
\]
なので$R \circ R \not\subset R $である.有向グラフで考えると,$1$と$3$は2本の矢印を通り辿り着けるが,その間には近道がない.
4.4 同値関係
定義 4.8
集合$X$上の関係$R$が同値関係 (equivalence relation)であるとは,$R$が反射的かつ対称的かつ推移的であるときにいう.この3つの条件をそれぞれ反射律 ,対称律 ,推移律という.
$R$が同値関係のとき,$a R b$ならば,$a$と$b$は$R$に関して同値であるという.
同値関係には$\sim$や$\equiv$という記号がよく使われる.このとき,$a$と$b$が同値ではないとき,$a \not\sim b$や$a \not\equiv b$と書く.
同値関係は「なんらかの意味で等しい」を意味する関係であり,これまでの「等しい($=$)」という概念を拡張している.まず「等しい($=$)」が実際に同値関係であることを確認する.
例 4.9
例4.2の集合$X$と$X$上の関係$R,S,T$を考える.これまでの結果をまとめると,以下の表が成り立つ:
$R,S,T$はそれぞれ,$=,\leq, \lt $という関係を表していたことを思い出そう.同値関係は「等しい」という概念を拡張したものなので,$=$だけが同値関係となるのは納得できるであろう.
次に,「なんらかの意味で等しい」ということを具体例で確認してみる.
| 関係 | 反射律 | 対称律 | 推移律 | 同値関係 |
|---|---|---|---|---|
| $R$ | ○ | ○ | ○ | ○ |
| $S$ | ○ | × | ○ | × |
| $T$ | × | × | ○ | × |
例 4.10
この教室にいる学生の集合を$X$とする.
今,$X$上の二項関係$\sim$を
\[
\sim =\{ (a,b) \in X^2 : a\mbox{と}b\mbox{の誕生月は同じである}\}
\]
で定義する.ただし,自分自身とも誕生月が同じであるとみなすことに注意する.これは反射律が成り立つことを意味する.また$a$と$b$の誕生月が同じであればもちろん$b$と$a$の誕生月は同じなので,対称律も成り立つ.最後に,$a$と$b$の誕生月が同じでかつ$b$と$c$の誕生月が同じであれば,$a$と$c$の誕生月も同じであるので,推移律も成り立つ.以上より,$\sim$は同値関係となる.
注意 4.11
例4.10のように,順序対$(a,b)$に同じ法則で二項関係を定義するとき,集合の形ではなく,次のような書き方をすることがある.「$X$上の二項関係$\sim$を
\[
a \sim b \iff a\mbox{と}b\mbox{の誕生月は同じである}
\]
で定義する」こちらの方が,上の集合の形で定義するよりわかりやすいだろう.意味は同じなので,どっちで書かれていても理解できるようにしよう.
次に,似たように定義した2つの二項関係が,片方は同値関係になり,もう片方はならない場合があることを見る.
例 4.12
$\mathbb{Z}$上の二項関係,$\sim_E$と$\sim_O$を
\begin{align*}
a \sim_E b & \iff a-b\mbox{が偶数}\\
a \sim_O b &\iff a-b\mbox{が奇数}
\end{align*}
で定義する.
後で証明する命題4.15を使うと$\sim_E$は同値関係となる.一方,$\sim_O$は同値関係ではない.実際,$1 \in \mathbb{Z}$に対し,$1-1=0$は奇数ではないので,$1 \not\sim_O 1$であり,反射律が成り立たない.また推移律も成り立たない.似たような定義でも同値関係になるかどうかはわからない.この2つの二項関係にはどういった差があるのか,なぜ同値関係の定義に$3$つの性質を必要とするのか.その理由は集合を「なんらかの意味で等しいもの」でグループ分けしたいからである.これは次回説明する.
任意の集合$X$に対して,恒等関係${\rm Id}_X$はいつでも同値関係であった.これとは別に,明らかに同値関係となるものがもう一つある.
例 4.13
集合$X$に対し,全体関係$X \times X$は同値関係である.この同値関係は集合の要素が全て「等しい」ということになる.この同値関係を$X$の自明な同値関係と呼ぶ.
4.5 合同式
同値関係の代表例の1つは整数に対する合同式である.定義 4.14
自然数$m$に対し,整数$a$と$b$が$m$を法 (module)として合同 (congruent)であるとは,$a-b$が$m$の倍数となるときにいう.
このとき,
\[
a \equiv_m b \mbox{または} a \equiv b \ ({\rm mod}\ m)
\]
と書く.
法$m$が文脈から明らかのときは,単に$a \equiv b$と書くこともある.
例えば,$5 \equiv_3 2 \equiv_3 -1$であり,これは$3$で割った余りが等しいという関係を表す.これは高校数学の発展として教科書に書かれている.
この合同式$\equiv_m$が実は同値関係であることを示そう.そのために,$\equiv_m$を$\mathbb{Z}$上の二項関係で再定義する.自然数$m$に対して,$m\mathbb{Z}=\{ mx : x \in \mathbb{Z}\}$,つまり$m$の倍数全体の集合とすると,合同式は$\mathbb{Z}$上の二項関係として
\[
a \equiv_m b \iff a-b \in m\mathbb{Z}
\]
で定義できる.例えば,$5-2=3 = 3 \cdot 1 \in 3 \mathbb{Z}$なので,$5 \equiv_3 2$である.
命題 4.15
$m$を自然数とする.$\mathbb{Z}$上の二項関係$\equiv_m$は同値関係である.
証明
(反射律) 任意の整数$a \in \mathbb{Z}$に対し,$a-a=0=m \cdot 0 \in m \mathbb{Z}$なので,$a \equiv_m a$が従い,$\equiv_m$は反射的である.
(対称律) 任意の整数$a,b \in \mathbb{Z}$で,$a \equiv_m b$となるものをとってくる.このとき,$a-b \in m \mathbb{Z}$であるので,ある整数$k$に対し,$a-b= m k$と書ける.$b-a=-mk=m (-k)$であり,$-k$は整数なので,$b-a \in m \mathbb{Z}$が従う.よって$b \equiv_m a$となり,$\equiv_m$は対称的である.
(推移律) 任意の整数$a,b,c \in \mathbb{Z}$で,$a \equiv_m b$かつ$b \equiv_m c$となるものをとってくる.このとき,$a -b, b-c \in m\mathbb{Z}$なので,ある整数$k$と$\ell$に対し,$a-b=mk, b-c=m\ell$と書ける. \[ a-c=(a-b)+(b-c)=mk+m \ell =m(k+\ell) \] となり,$k+\ell$は整数であるので,$a-c \in m\mathbb{Z}$が従う.よって$a \equiv_m c$となり,$\equiv_m$は推移的である.
以上より,$\equiv_m$は反射律,対称律,推移律が成り立つので,同値関係である.