5回目：同値類と商集合

集合$X$上の二項関係$R$は反射律，対称律，推移律の3つを満たすとき，同値関係と呼んでいた．同値関係は「なんらかの意味で等しい」を意味する関係であった．同値関係のこの$3$つの性質は，集合をこの「なんらかの意味で等しい」もので分割するために必要な性質である．

5.1 集合の分割

定義 5.1

空でない集合$X$の分割 (partition)とは，$X$の部分集合族$P \subset 2^{X}$で条件

$\emptyset \notin P$
任意の$x \in X$に対して，$x \in A$となる$A \in P$が存在する
任意の$A,B \in P$に対して，$A \neq B$ならば$A \cap B =\emptyset$

を満たすときにいう．$P$の元を分割のブロック (block)という．

注意 5.2

(2)の条件は任意の$x \in X$に対し，$x\in \bigcup_{A \in P} A$が成り立つことを意味し，これは$X=\bigcup_{A \in P} A$と同値である．また２つの集合$A$と$B$が互いに素とは，$A \cap B = \emptyset$を満たすときにいい，$A \cap B \neq \emptyset$を満たすときは，交わるという．つまり条件(3)は$P$の相異なる元は互いに素ということになる．

例 5.3

整数$0 \leq r \leq 2$に対し，整数全体の集合$\mathbb{Z}$の部分集合$A_r$を \[ A_r=\{a \in \mathbb{Z} : \mbox{$a$を$3$で割った余りが$r$} \}\] と定義し，$P=\{A_0,A_1,A_2\}$とする．ここで，$a$を$3$で割った余りとは，整数$k$と整数$0 \leq \ell \leq 2$を用いて$a=3k+\ell$と表したときの$\ell$のことである．$0 \in A_0, 1 \in A_1, 2 \in A_2$より$\emptyset \notin P$から条件(1)が成り立つ．また，任意の$x \in \mathbb{Z}$に対し，ある整数$k$が存在して$x=3k$または$x=3k+1$または$x=3k+2$が成り立つが．$x=3k$ならば$x \in A_0$，$x=3k+1$ならば$x \in A_1$，$x=3k+2$ならば$x \in A_2$となるので条件(2)が成り立つ．最後に，$A_0 \cap A_1 = \emptyset, A_0 \cap A_2 =\emptyset, A_1 \cap A_2=\emptyset$であるので条件(3)が成り立つ．以上より$P$は$\mathbb{Z}$の分割である．

5.2 同値類と商集合

集合の分割は同値関係から構成することができる．そのために同値類と商集合という概念を導入する．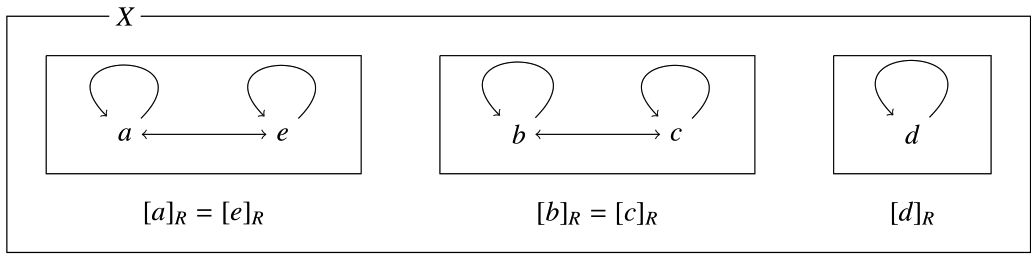

定義 5.4

$\sim$を集合$X$上の同値関係とする．各$x \in X$に対して，$x$と同値となる元全体の集合$\{y \in X : x \sim y\}$を$x$の$\sim$による同値類 (equivalent class)といい，$[x]_{\sim}$や単に$[x]$で表す．このとき，$x$は$[x]_{\sim}$の代表元 (representative element)という．さらに$\sim$の同値類全体の集合$\{[x]_\sim : x \in X\}$を$X$の$\sim$による商集合 (quotient set)といい，$X/{\sim}$で表す．また$X$の部分集合$S$が$X/{\sim}$の各元（同値類）の代表元をちょうど１つずつ含むとき，$S$を$\sim$の完全代表系 (complete set of representative elements)と呼ぶ．

同値類は「なんらかの意味で等しい」ものの集まりであり，商集合はその集まりごとの集合である．例を見て考えてみよう．

例 5.5

集合$X=\{a,b,c,d,e\}$上の二項関係 \[ R=\{(a,a),(b,b),(c,c),(d,d),(e,e),(a,e),(e,a),(b,c),(c,b)\} \] を考える．これが同値関係となっていることの確認は各自で行おう．このとき，$R$の同値類は \[ [a]_R=[e]_R=\{a,e\}, [b]_R=[c]_R=\{b,c\}, [d]_R=\{d\} \] である．よって$A$の$R$による商集合は \[ X/R=\{ [a]_R,[b]_R,[c]_R,[d]_R,[e]_R\}=\{[a]_R,[b]_R,[d]_R\}=\{\{a,e\},\{b,c\},\{d\}\} \] となる．この商集合$X/R$が$X$の分割になっていることも簡単に確認できる．また集合$\{a,b,d\} \subset X$は同値関係$R$の完全代表系である．完全代表系は一意に定まるとは限らず，例えば$\{a,c,d\}$も$R$の完全代表系である．この同値類や商集合は元の集合が有限集合であれば有向グラフを書いて想像しやすい．実際，同値関係$R$に対応する有向グラフは

であり，いくつかの繋がっている島に分かれている．この各島のことを連結成分 (connected component)と呼ぶ．同値関係の有向グラフは各連結成分が自明な同値関係を表しており，それぞれが$R$の同値類と対応している．そして商集合はこの連結成分の集合とみなすことができる．さらに，各頂点はそれぞれの連結成分が表す同値類の代表元であり，各連結成分から1つずつ頂点をとったものが完全代表系である．

注意 5.6

$\sim$を集合$X$上の同値関係とすると，任意の$a,b \in X$に対し， \[ a \sim b \Leftrightarrow [a]=[b] \] が成り立つ．これは同値関係が対称的であることから従う（証明略）．

例 5.7

前回定義した自然数$m$を法とした$\mathbb{Z}$上の合同式 \[ a \equiv_{m} b \Leftrightarrow a-b \in m\mathbb{Z} \] を考える．ここで，$m\mathbb{Z}=\{mx : x\in \mathbb{Z}\}$である．この合同式は同値関係であった．簡単のため$m=3$とし，単に$\equiv$と書く．例えば，$5 \equiv 2$であるので，$[5]_{\equiv}=[2]_{\equiv}$であるが，この同値類を正確に求めるとどういった集合となるのだろうか．また商集合はどのようなものか．実際，例5.3で考えた集合$A_0,A_1,A_2$を考えると．$[2]_\equiv=A_2$である．なぜなら任意の整数$a \in A_2$は$a=3k+2$（$k$は整数）と表せ，$a-2=(3k+2)-2=3k \in 3 \mathbb{Z}$，つまり$a \equiv 2$であるので$a \in [2]_\equiv$である．これは$A_2 \subset [2]_\equiv$を意味する．逆に任意の整数$a \in [2]_{\equiv}$をとると，$a-2 \in 3 \mathbb{Z}$なので，$a-2=3k$（$k$は整数）と表せ，$a = 3k+2$からこれは$a \in A_2$となる．つまり$[2]_{\equiv} \subset A_2$となり，結局$[2]_\equiv =A_2$となる．同様に，$[1]_{\equiv}=A_1$と$[0]_{\equiv}=A_0$も証明できる．またどの整数も$A_0,A_1,A_2$のいずれかの元なので，商集合は \[ \mathbb{Z}/ \hspace{-1mm}\equiv \ =\{ [x]_{\equiv} : x\in \mathbb{Z}\}= \{A_0,A_1,A_2\} \] となる．さらに集合$\{1,2,3\} \subset \mathbb{Z}$は合同式$\equiv$の完全代表系である．

5.3 同値関係と分割

例で見た通り，ここでどんな同値関係に対しても商集合が分割となっていることを示そう．

命題 5.8

$\sim$を集合$X$上の同値関係とする．商集合$X/{\sim}$は$X$の分割である．

証明

(1) 勝手な同値類$[x] \in X/{\sim}$をとる．ただし$x \in X$である． $\sim$は同値関係なので反射的であり，$x \sim x$だから，$x \in [x]$である．ゆえに $[x] \neq \emptyset$である．よって$\emptyset \notin X/{\sim}$となる．

(2) 任意の$x \in X$に対して，$A=[x] \in X/{\sim}$とすれば，$\sim$の反射性より$x \sim x$となり，$x \in A \in X/{\sim}$である．

(3) 任意の$A,B \in X/{\sim}$をとる．対偶を証明するために$A \cap B \neq \emptyset$を仮定する．$X/{\sim}$の定義から，ある$a \in X$と$b \in X$に対して，$A =[a]$と$B=[b]$と書ける．$A \cap B \neq \emptyset$から，ある$c \in X$で$c \in A$かつ$c \in B$を満たすものが存在する．つまり$c \in [a]$かつ$c \in [b]$である．同値類の定義からこれは$a \sim c$かつ$b \sim c$を意味する．$\sim$は対称的なので$c \sim b$も成り立つ．さらに$\sim$は推移的であるので，$a \sim c$かつ$c \sim b$から$a \sim b$が従う．よって$[a]=[b]$，つまり$A=B$となる．対偶を考えると，結局$A \neq B$ならば$A \cap B = \emptyset$が成り立つ．

以上より$X/{\sim}$は$X$の分割である．

この命題から集合$X$の同値関係を1つ与えると，それに対応した$X$の分割が1つ得られることがわかった．逆に$X$の分割を1つ与えると，それに対応した同値関係も得ることができる．

命題 5.9

集合$X$とその分割$P$に対し，$X$上の関係$\sim $を以下のように定義する：\[ a \sim b \Leftrightarrow \mbox{$a \in A$かつ$b \in A$を満たすブロック$A \in P$が存在する}. \] このとき，$\sim$は同値関係である．

証明

（反射律）$P$は$X$の分割なので，分割の定義(2)から任意の$a \in X$に対し，$a \in A$となる$A \in P$が存在する．したがって$\sim$の定義から$a \sim a$，つまり$\sim$は反射的である．

（対称律）任意の$a,b \in X$で$a \sim b$となるものをとる．このとき，$\sim $の定義から，$a \in A$かつ$b \in A$を満たす$A \in P$が存在する．つまりある$A \in P$に対し，$b \in A$かつ$a \in A$となるので，$b \sim a$が成り立ち，$\sim$は対称的である．

（推移律）任意の$a,b,c \in X$で$a \sim b$かつ$b \sim c$となるものをとる．このとき，$\sim$の定義から，ある$A \in P$に対し，$a \in A$かつ$b \in A$，さらにある$B \in P$に対し，$b \in B$かつ$c \in B$が成り立つ．$b \in A$かつ$b \in B$より，$b \in A \cap B$が成り立ち，特に$A \cap B \neq \emptyset$である．分割の定義(3)の対偶を考えると，$A = B$が従う．よって$a \in A$かつ$c \in A$となり，$a \sim c$が成り立ち，$\sim$は推移的である．

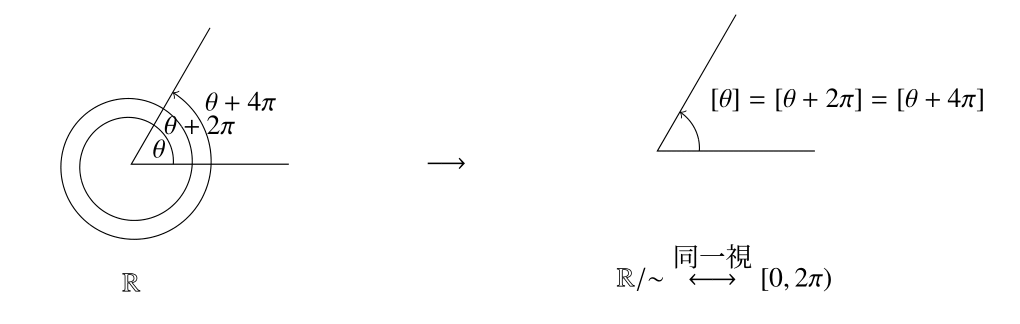
以上より，$\sim$は同値関係である．

この2つの命題から集合$X$の同値関係を与えることと，分割を与えることは同じ操作であることがわかる．この分割を与えるという目的のため，同値関係の定義の３つの性質が必要となる．

5.4 一般角

高校数学で一般角を考えたとき，$2 \pi$（ラジアン）の整数倍だけ違うものは同じ角度であると見なす（同一視する）と便利なときがあった．実際，角度$\theta$と整数$n$に対し， \[ \sin \theta = \sin (2 n \pi + \theta),\ \ \ \ \ \cos \theta = \cos (2n \pi + \theta) \] が成り立つ．このように何かと何かを同一視するときに同値類が使われる．実数の集合$\mathbb{R}$上の二項関係を \[ x \sim y \Leftrightarrow x-y \in \{ 2 n \pi : n \in \mathbb{Z}\} \] で定義する．この関係が同値関係となることの証明は演習問題とする．このとき，部分集合$[0, 2\pi)=\{ \theta \in \mathbb{R} : 0 \leq \theta \lt 2\pi\} \subset \mathbb{R}$は同値関係$\sim$の完全代表系である．これを確かめるためには次の2つを示せばよい．

任意の$x,y \in [0, 2\pi)$に対し，$x \neq y$ならば$[x] \neq [y]$である．
任意の$x \in \mathbb{R}$に対し，ある$y \in [0,2\pi)$が存在して，$x \in [y]$である．

証明

（1）任意の$x,y \in [0, 2\pi)$に対し$x > y$とすると$0 \lt x-y \lt 2\pi$である．これは$x \not\sim y$を意味する．特に，$[x] \neq [y]$である．

（2）任意の$x \in \mathbb{R}$に対し，ある整数$n$で$ 2 n \pi \leq x \lt (2n+2)\pi$となるものが存在する．$y=x-2n\pi$とすると， $0 \leq y \lt 2 \pi$が成り立つ．このとき，$x-y=2n \pi$となるので，$x \sim y$である．よってこの$y$に対し，$x \in [y]$が成り立つ．

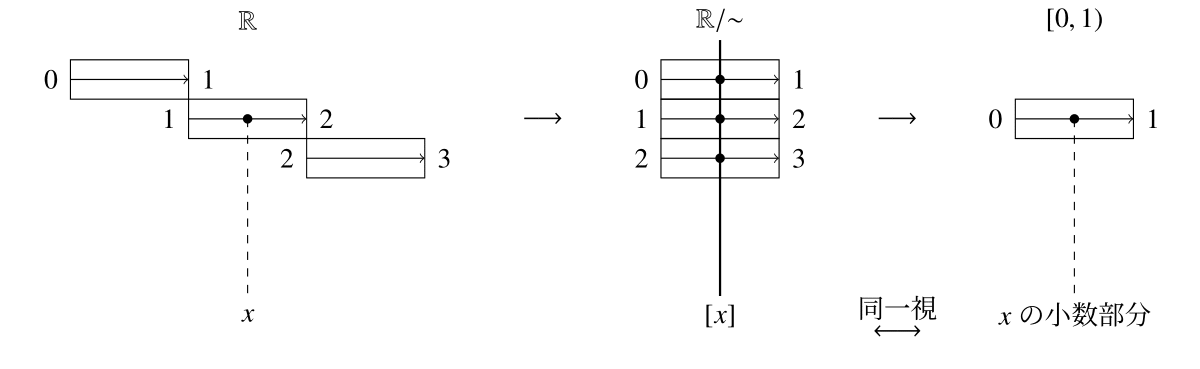
今，実数の集合$\mathbb{R}$を一般角全体の集合だと認識しよう．すると商集合$\mathbb{R}/{\sim}$と完全代表系$[0,2\pi)$を同一視することで，一般角$\theta \in \mathbb{R}$の$\sim$による同値類$[\theta] \in \mathbb{R}/{\sim}$は一周内の角度と見なすことができる．

上記の$\sin$と$\cos$の一般角に関する式を商集合の言葉で書くと，以下のようになる： \[ x,y \in [\theta] \Rightarrow \sin x = \sin y, \cos x = \cos y. \]

5.5 小数部分

同一視の違う例を見てみよう．実数の集合$\mathbb{R}$上の二項関係を \[ x \sim y \Leftrightarrow x-y \in \mathbb{Z} \] で定義する．この関係は同値関係である．このとき，部分集合$[0,1) \subset \mathbb{R}$は同値関係$\sim$の完全代表系である（確かめよ）．つまり，商集合$\mathbb{R}/{\sim}$は$[0,1)$と同一視できる．この同一視を図でイメージしてみよう．$\mathbb{R}$を数直線のテープだと思う．便宜上テープの左端を$0$としておき，長さ$1$ずつこのテープを切っていく．ただし，切ったテープの右端はそのテープに含まれないとする．今，この切ったテープを縦に並べていく．すると，実数$x \in \mathbb{R}$の$\sim$による同値類$[x]$はこの縦長のテープの左端からの距離を表すことになる．下図の縦の線がこの$[x]$を表している．一方，切ったテープを上に重ねていくこと考える．すると（無限の厚みはあるが）長さ1のテープであることには変わりない．これは集合$[0,1)$を表している．したがって，商集合$\mathbb{R} / \sim$は完全代表系$[0,1)$と同一することで，実数$x \in \mathbb{R}$の$\sim$による同値類$[x] \in \mathbb{R}/{\sim}$は$0$以上$1$未満の実数とみなすことができる．特にこれは，$x$の小数部分を表している．例えば，$[1.3]$は$0.3$，$[\pi]$は$0.141592\cdots$を表していると考えることができる．ただし，負の数の小数部分は注意が必要（$[-0.2]$の小数部分は$0.8$である）．

情報数理B