6回目：順序関係と順序集合
6.1 前順序
$\mathbb{Z}$上の関係$\leq$（以下）は条件- （反射律） $\forall x \in X ( (x,x) \in R) \iff {\rm Id}_X \subset R$
- （推移律） $\forall a,b,c \in X ( (aRb \land bRc) \rightarrow aRc) \iff R \circ R \subset R$
定義 6.1
集合$P$上の関係$\leq_P$は反射律と推移律を満たすとき，前順序 (preorder)であるという．
例 6.2
$P$をこの講義を受けている学生の集合とする．$P$上の関係として
\[
a \leq_P b \Leftrightarrow \mbox{$a$のテストの点数は$b$以下である}
\]
と定義する．
任意の$a \in P$に対し，$a$のテストの点数は自身の点数以下であるので，$a \leq_P a$，つまり反射律が成り立つ．また$a \leq_P b$と$b \leq_P c$は「$a$は$b$の点数以下」，「$b$は$c$の点数以下」を意味し，「$a$は$c$の点数以下」となるので，これは$a \leq_P c$を意味する．よって推移律も成り立つ．以上より$\leq_P$は前順序である．
6.2 反対称的な関係
前順序は$\mathbb{Z}$上の「$\leq$」という概念を抽象化しているが，まだ数学的な「順序」としては不十分である． 例6.2に出てきた$\leq_P$を考えると，$a \leq_P b$かつ$b \leq_P a$は「$a$と$b$が同じ点数」を意味し，$a$と$b$が同じ人，つまり$a=b$であるとは限らない．「順序が等しい」と「要素が等しい」が違う意味を持つことになる．一方で$\mathbb{Z}$上の「$\leq$」は$a \leq b$と$b \leq a$という順序が成り立てば，$a$と$b$は同じ数字，つまり$a=b$となる．この性質は等号を示すのに非常に重要である．まずはこの性質を「関係」の性質として定義する．定義 6.3
集合$X$上の関係$R$が反対称的 (antisymmetric)であるとは，任意の$a,b \in X$に対して$(a,b) \in R$かつ$(b,a) \in R$ならばいつでも$a=b$であるときにいう．つまり，
\[
\mbox{$R$が反対称的である} \iff \forall a,b \in X ( aRb \land bRa \rightarrow a=b) \iff R \cap R^{-1} \subset {\rm Id}_X
\]
である．この条件を反対称律という．「反対称的」は「対称的ではない」とは違う意味であることに注意する．
例6.2の「$\leq_P$」はもし同じ点数を取った人が複数人いれば反対称的ではない．
一方で$\mathbb{Z}$上の「$\leq$」は反対称的である（むしろ「$\leq$」の性質を抜き出したのだから当たり前である）．
もう少し例を見ておこう．
例 6.4
$X=\{1,2,3\}$とし，$X$上の関係を
\[
R=\{ (1,1),(1,2),(1,3), (3,2), (3,3)\}
\]
とすると，$R$と$R^{-1}$の有効グラフは次のようになる．
よって$R\cap R^{-1}=\{(1,1),(3,3) \} \subset {\rm Id}_X$となり$R$は反対称的である．関係が反対称的であることと，有効グラフの異なる２頂点には両方向の矢印がないことは同値である．
6.3 半順序
定義 6.5
集合$P$上の関係$\leq_P$は反射律，推移律，反対称律を満たすとき，半順序 (partial order)，または単に順序 (order)という．半順序の記号としては$\leq_P,\preceq_P$などがよく使われる．また半順序$\leq_P$を備えた集合$(P,\leq_P)$のことを半順序集合 (partially ordered set, poset)，または単に順序集合 (ordered set)という．半順序$\leq_P$が文脈から明らかなときは，$(P,\leq_P)$を単に$P$で表すこともある．半順序集合$(P,\leq_P)$と$a,b \in P$に対し，$a \leq_P b$かつ$a \neq b$のときは，$a \lt_P b$と書き，$a \leq_P b$や$a\lt_P b$を$b \geq_P a$や$b>_P a$と書いたりする．日本語では$\leq$と同様に以下，以上，より小さい，より大きいなどで表現する．
$\mathbb{Z}$上の関係$\leq$は半順序であり，$(\mathbb{Z},\leq)$は半順序集合となる．
一方で，例6.2の$\leq_P$は反対称的ではないので半順序とはならない．
半順序の具体例を見てみる．
例 6.6
$P$をこの講義を受けている学生の集合とする．$P$上の関係として
\[
a \leq_P b \Leftrightarrow \mbox{$a$さんの学籍番号は$b$さんの学籍番号以下である}
\]
と定義する．これが反射律と推移律を満たすことは容易に確かめられる．一方で，東邦大学内では，学籍番号は異なる人には異なる番号が与えられているので，$a \leq_P b$かつ$b \leq_P a$であれば，$a=b$である．よって$\leq_P$は半順序である．
自然数の集合$\mathbb{N}$に対し，$(\mathbb{N}, \leq)$も半順序集合であるが，同じ集合でも異なる順序を定義することができる．$\mathbb{Z}$上の順序で代表的な例を1つ見よう．
例 6.7
$\mathbb{N}$上の二項関係を
\[
a \leq_{\mathbb{N}} b \Leftrightarrow \mbox{$a$は$b$の約数である}
\]
で定義する．この関係が半順序となることを見る．
（反射律）任意の自然数$x \in \mathbb{N}$に対し，$x$は$x$の約数であるので，$x \leq_{\mathbb{N}} x$が成り立つ．
（推移律）任意の自然数$x,y,z \in \mathbb{N}$で$x \leq_{\mathbb{N}} y, y \leq_{\mathbb{N}} z$を満たすものをとる（$x \leq_{\mathbb{N}} y \leq_{\mathbb{N}} z $とは書かない）．このとき，ある自然数$k$が存在して，$y=kx$と書ける．同様にある自然数$\ell$が存在して$z=\ell y$と書ける．すると \[ z=\ell y = \ell ( kx) = (\ell k) x \] となり，$\ell k$は自然数なので，$x$は$z$の約数となる．つまり$x \leq_{\mathbb{N}} z$が成立する（推移律が成り立つことがわかると$x \leq_{\mathbb{N}} y \leq_{\mathbb{N}} z $と書いてもよい）．
（反対称律）任意の自然数$x,y \in \mathbb{N}$で$x \leq_{\mathbb{N}} y, y \leq_{\mathbb{N}} x$を満たすものをとる．このとき， ある自然数$k$と$\ell$が存在して，$y=kx, x= \ell y$と書ける．すると \[ x=\ell y = \ell ( kx) = (\ell k) x \] となり，$x$が自然数なので，$\ell k=1$，さらに$\ell, k$も自然数なので$\ell=k=1$となる．これは$x=y$を意味する．
以上より，$\leq_{\mathbb{N}}$は反射律，推移律，反対称律を満たすので，$\mathbb{N}$上の順序となる．
$\mathbb{N}$において，通常の$\leq$という順序ではどんな自然数にも順序が付いていた．つまり任意の自然数$x,y \in \mathbb{N}$に対し，
$x \leq y$または$x \geq y$が成り立つ．しかし，例6.7の順序$\leq_{\mathbb{N}}$では順序が付いていない要素が存在する．
実際，$2$と$3$は互いに約数ではないので，$2 \leq_{\mathbb{N}} 3$でも$2 \geq_{\mathbb{N}} 3$でもない．
（反射律）任意の自然数$x \in \mathbb{N}$に対し，$x$は$x$の約数であるので，$x \leq_{\mathbb{N}} x$が成り立つ．
（推移律）任意の自然数$x,y,z \in \mathbb{N}$で$x \leq_{\mathbb{N}} y, y \leq_{\mathbb{N}} z$を満たすものをとる（$x \leq_{\mathbb{N}} y \leq_{\mathbb{N}} z $とは書かない）．このとき，ある自然数$k$が存在して，$y=kx$と書ける．同様にある自然数$\ell$が存在して$z=\ell y$と書ける．すると \[ z=\ell y = \ell ( kx) = (\ell k) x \] となり，$\ell k$は自然数なので，$x$は$z$の約数となる．つまり$x \leq_{\mathbb{N}} z$が成立する（推移律が成り立つことがわかると$x \leq_{\mathbb{N}} y \leq_{\mathbb{N}} z $と書いてもよい）．
（反対称律）任意の自然数$x,y \in \mathbb{N}$で$x \leq_{\mathbb{N}} y, y \leq_{\mathbb{N}} x$を満たすものをとる．このとき， ある自然数$k$と$\ell$が存在して，$y=kx, x= \ell y$と書ける．すると \[ x=\ell y = \ell ( kx) = (\ell k) x \] となり，$x$が自然数なので，$\ell k=1$，さらに$\ell, k$も自然数なので$\ell=k=1$となる．これは$x=y$を意味する．
以上より，$\leq_{\mathbb{N}}$は反射律，推移律，反対称律を満たすので，$\mathbb{N}$上の順序となる．
定義 6.8
$(P,\leq_P)$を半順序集合とする．$a,b \in P$に対し，$a \leq_P b$ではないとき，$a \not\leq_P b$と書く．$\not\geq_P,\not<_P,\not>_P$も同様に定義する．$a \not\leq_P b$かつ$a \not\geq_P b$が成り立つとき，$a$と$b$は比較不可能 (incomparable)であるという．一方，$a \leq_P b$または$a \geq_P b$が成り立つときは，$a$と$b$は比較可能 (comparable)であるという．また半順序集合$(P,\leq_P)$は任意の$a,b \in P$に対し，$a$と$b$が比較可能であるとき，全順序集合 (totally ordered set)といい，$\leq_P$を全順序 (total order)という．
半順序集合$(\mathbb{N}, \leq)$は全順序集合であるが，例6.7の半順序集合$(\mathbb{N},\leq_\mathbb{N})$は全順序集合ではない．
また「$\leq$」では$\not\leq$と$>$は同じ意味であったが，「$\leq_{\mathbb{N}}$」では$\not\leq_{\mathbb{N}}$だったとしても，$>_{\mathbb{N}}$になるとは限らない．実際，$2 \not\leq_{\mathbb{N}} 3$であるが，$2 >_{\mathbb{N}} 3$ではない．
6.4 ハッセ図
半順序は集合上の関係なので，集合が有限であれば，これまで通り有向グラフを使って表すことができる．しかし，そのまま書くと辺の個数が多すぎたりして見にくくなることがある．そこで半順序の3つの条件が成り立つことを意識して，もう少し単純な図として書くことにする．まず，集合$P=\{1,2,3,4,5\}$上の関係 \[ \leq_P:=\{(1,1),(1,3),(1,4),(1,5),(2,2),(2,3),(2,4),(2,5),(3,3),(3,4),(3,5),(4,4),(5,5)\} \] を考える．これが半順序となることは各自確かめよう． この半順序は$13$個の$a \leq_P b$という情報からできているが，$\leq_P$を復元するのに本当にこれだけの情報がいるであろうか． 例えば，反射律が成り立つため，どんな$i \in P$に対しても，$i \leq_P i$となる．したがって，半順序となることを知っていれば$i \leq_P i$という情報は書かなくてもわかる． さらに，この半順序では，$1 \leq_P 3, 1 \leq_P 5, 3 \leq_P 5$という情報があるが，推移律が成り立つため，$1 \leq_P 3, 3 \leq_P 5$がわかっていれば，$1 \leq_P 5$が従うので，これもなくてよい．以上のことを考えると，実は$\leq_P$は \[ 1 \leq_P 3, 2 \leq_P 3, 3 \leq_P 4, 3 \leq_P 5\] という4個の情報さえあれば復元可能である． なお，反対称律から$\leq_P$ではなく$\lt_P$を考えれば十分なのもわかるであろう． この必要最低限の情報を定義する．
定義 6.9
$(P,\leq_P)$を半順序集合とし，$a \lt_P b$となる$a,b \in P$をとる．もし$a \lt_P c$かつ$c \lt_P b$となる$c \in P$が存在しなければ，$a \lt_P b$という関係を被覆関係 (cover relation)といい，$a \lessdot_P b$と書く．
つまり被覆関係とは，中間の要素がない関係のことである．
先ほどの例だと，$\leq_P$は
\[
1 \lessdot_P 3, 2 \lessdot_P 3, 3 \lessdot_P 4, 3\lessdot_P 5
\]
という被覆関係全体から復元される．
それではこの被覆関係から次の手順で有向グラフを書いてみよう．
- 頂点を順序が大きいものが上にくるように書く（反対称律から必ずこのように置ける）．
- 各被覆関係に対して小さいものから大きいものへ矢印を書く．
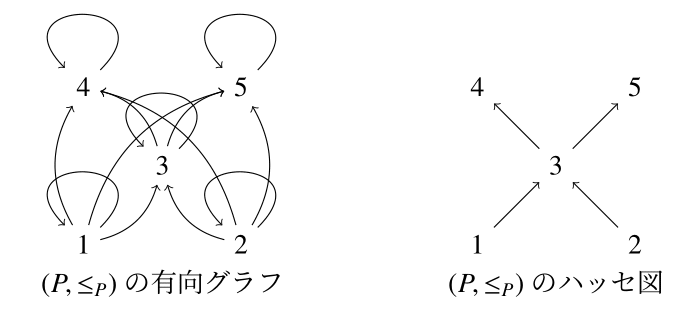
例 6.10
全順序のハッセ図は非常に単純である．実際，一直線になる．$P=\{1,2,3\}$とし，通常の意味での「$\leq$」を考えると，$(P,\leq)$は全順序である．このハッセ図は以下の通りになる．
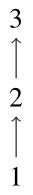
例 6.11
$n$を自然数とし，$P$を$n$の約数全体の集合とする．$P$上の関係を
\[
a \leq_{P} b \Leftrightarrow \mbox{$a$は$b$の約数である}
\]
で定義する．例6.7と同様に，この関係も順序関係であることがわかる．$n=12$のときに，$(P,\leq_P)$のハッセ図を書くと次のようになる．
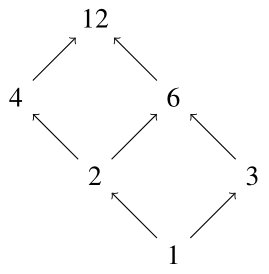
例 6.12
半順序の代表例を1つ紹介する．
集合$X=\{1,2,3\}$の冪集合$P=2^X$上の二項関係を
\[
A \leq_P B \Leftrightarrow A \subset B
\]
で定義する．このとき，$\leq_P$は半順序である（確かめよ）．ここではわざわざ$\leq_P$で置き直したが，基本は包含関係による順序として$(P,\leq_P)$の代わりに$(P, \subset)$と書く．
このときの$(P,\subset)$のハッセ図は次のとおりである．
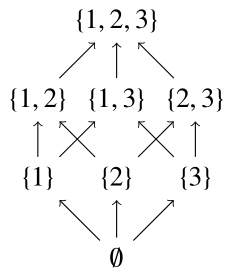このハッセ図をよく見ると立方体の骨組み（辺と頂点）となっていることがわかるであろう．それでは$Y=\{1,2,3,4\},Q=2^Y$とし，包含関係による半順序集合$(Q, \subset)$のハッセ図を機械的に書いたものと，少し場所を意識して書いたものの２通り書く．
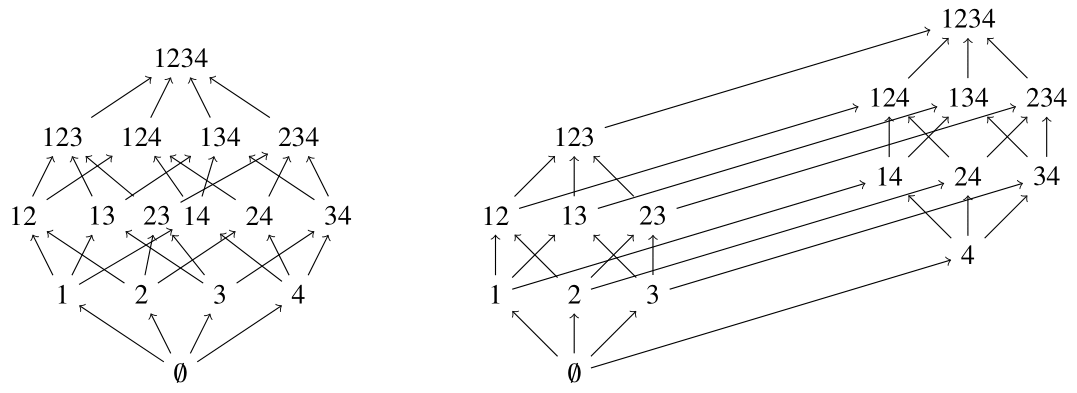右の図は，2つの立方体（$(P, \subset)$のハッセ図）を繋いだ形をしている．立方体は2つの正方形を繋いだ形であった．実は，$(Q, \subset)$のハッセ図は$4$次元の立方体（$4$次元超立方体）の骨組みとなっている．より一般に$[n]:=\{1,2,\ldots,n\}, P_n=2^{[n]}$とすると，半順序$(P_n,\subset)$のハッセ図は
$n$次元超立方体 (hypercube)の骨組みとなる．