7回目：最大・最小/極大・極小/上界・下界/上限・下限
7.1 極大・極小/最大・最小
これまで，最大や最小という言葉は自然と用いてきた．その用語を順序集合において厳密に定義する．定義 7.1
$(P,\leq_P)$を順序集合，$M$を$P$の空でない部分集合とする．このとき，
- $a \lt_P x$となる$x \in M$が存在しない$M$の元$a$を$M$の極大元 (maximal element)という．
- $x \lt_P b$となる$x \in M$が存在しない$M$の元$b$を$M$の極小元 (minimal element)という．
例 7.2
$X=\{1,2,3\}, P=2^X$とし包含関係による順序集合$(P, \subset)$，
さらに$P$の部分集合として\[M=\{\{1\},\{2\},\{3\}, \{1,2\}\}\]を考える．
このとき，$M$の極大元は$\{1,2\}$と$\{3\}$であり，極小元は$\{1\},\{2\},\{3\}$である．
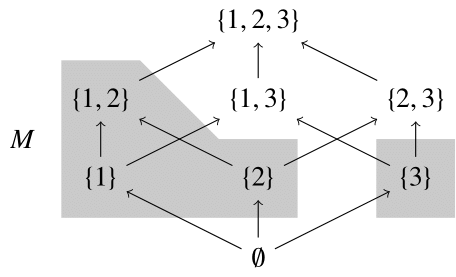
このように，- 極大（小）元は複数存在することがある
- 極大かつ極小となる元が存在することがある
命題 7.3
$(P,\leq_P)$を順序集合，$M$を$P$の空でない部分集合とする．$a,b \in M$が$M$の異なる極大（小）元のとき，$a$と$b$は比較不可能である．
証明
背理法で証明する．極大元$a$と$b$が比較可能であったとすると，$a \leq_P b$または$a \geq_P b$が成り立つ．$a \leq_P b$としてよい．特に，$a \neq b$であるので，$a \lt_P b$である．しかし，$a$は$M$の極大元なので，$a \lt_P x$となる$x$は$M$に存在しない．よって矛盾が起こるので，$a$と$b$は比較不可能である．
極小元の場合も同様に証明できる．
上の例では極大元，極小元の両方が存在していたが，存在しない場合もある．存在しない例はあとで見るが，ここでは有限集合であればいつでも極大（小）元を持つことを見る．
極小元の場合も同様に証明できる．
命題 7.4
$(P,\leq_P)$を順序集合とし，$M$を$P$の空でない有限部分集合とする．このとき，$P$は極大（小）元を少なくとも1個持つ．
証明
$M$の元の個数を$n$とし，$n$に関する帰納法で証明する．
$n=1$のときは，$M=\{a\}$とすると，$a \lt_P x$となる$M$の元$x$が存在しないので，$a$は極大元である．
$n \geq 2$とする．$M$の元$a$を1つ選び，$N=M \setminus \{a\}$とすると，$N$の元の個数は$n-1$である．よって，帰納法の仮定から$N$は極大元を持つ．それを$b$とする．
$b$が$M$の極大元であれば，証明は完結する．
$b$が$M$の極大元でなければ，$b \lt_P x$となる，$x \in M$が存在する．$b$は$N$の極大元であるので，$x \notin N$である．つまり，$x=a$である．特に，$a$は$M$の極大元となっている．実際，$a$が$M$の極大元でなければ，$a \lt_P y$となる$y \in M$が存在するが，これは$y \in N$であり，$b \lt_P a \lt_P y$となるので，$b$が$N$の極大元であることに矛盾する．
以上より，$M$は極大元を持つ．
極小元の場合も同様に証明できる．
極小元の場合も同様に証明できる．
定義 7.5
$(P,\leq_P)$を順序集合，$M$を$P$の空でない部分集合とする．このとき，
- 任意の$x \in M$に対して，$x \leq_P a$となる$M$の元$a$を，$M$の最大元 (maximum element)といい，$\max(M)$で表す．
- 任意の$x \in M$に対して，$b \leq_P x$となる$M$の元$b$を，$M$の最小元 (minimum element)といい，$\min(M)$で表す．
例 7.6
$X=\{1,2,3\}, P=2^X$とし包含関係による順序集合$(P, \subset)$，さらに$P$の部分集合として\[M=\{\{1\},\{2\},\{1,2\}\}\]を考える．
このとき，$M$の最大元は$\{1,2\}$であり，最小元は存在しない．
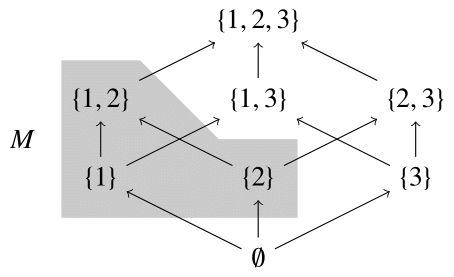
このように，
- （有限集合であったとしても）最大（小）元は存在するとは限らない
命題 7.7
順序集合$(P,\leq_P)$に対して，空でない$P$の部分集合$M$の最大（小）元は，存在すれば唯一である．また最大（小）は極大（小）元である．
証明
$M$の最大元が2個存在すると仮定する．
そこで，$a_1,a_2 \in M$（ただし$a_1 \neq a_2$）を$M$の最大元とする．$a_1$は最大元なので，任意の$x \in M$に対して，$x \leq_P a_1$，特に$a_2 \leq_P a_1$である．同様に，$a_2$も最大元なので，任意の$x \in M$に対して，$x \leq_P a_2$，特に$a_1 \leq_P a_2$である．
ところが，$\leq_P$は順序関係であるので，反対称律が成り立つ．これは$a_1=a_2$を意味し，矛盾．
よって$M$の最大元は，存在すれば唯一である．
また，$a$を$M$の最大元であるとする．$a$が$M$の極大元でないと仮定すると，$a \lt_P x$となる$x \in M$が存在する．しかし，$a$は$M$の最大元であるので，任意の$y \in M$に対し，$y \leq_P a$が成り立つ．特に$x \leq_P a$である．よって$x \leq_P a \lt_P x$となり，矛盾する．以上より，$a$は極大元である．
最小元の場合も同様に証明できる．
最小元の場合も同様に証明できる．
7.2 上界・下界/上限・下限
定義 7.8
$(P,\leq_P)$を順序集合，$M$を$P$の空でない部分集合とする．このとき，
- 任意の$x \in M$に対して，$x \leq_P a$となる$P$の元$a$を，$M$の$P$における上界 (upper bound)という．$M$の上界の全体を$U(M)$，つまり \[ U(M)=\{ a \in P : \mbox{すべての$x \in M$に対し$x \leq_P a$}\} \] とする． また，任意の$x \in M$に対して，$b \leq_P x$となる$P$の元$b$を，$M$の$P$における下界 (lower bound)という． $M$の下界の全体を$L(M)$，つまり \[ L(M)=\{ b \in P : \mbox{すべての$x \in M$に対し$b \leq_P x$}\} \] とする．
- $M$が$P$において上界をもつ，つまり$U(M)\neq \emptyset$のときは，上に有界といい，下界をもつ，つまり$L(M) \neq \emptyset$のときは，下に有界という．さらに$M$が上界も下界ももつときは，有界という．
- $U(M) \neq \emptyset$かつ$\min (U(M))$が存在するとき，これを最小上界 (least upper bound)，または上限 (supremum)といい，$\sup(M)$で表す． また，$L(M) \neq \emptyset$かつ$\max (L(M))$が存在するとき，これを最大下界 (greatest lower bound)，または下限 (infinum)といい，$\inf(M)$で表す．
例 7.9
$X=\{1,2,3\}, P=2^X$とし包含関係による順序集合$(P, \subset)$，
さらに$P$の部分集合として\[M=\{\{1\},\{2\},\{1,2\}\}\]を考える．
このとき，
$M$の上界は$\{1,2\}$と$\{1,2,3\}$であり，上限は$\{1,2\}$である．一方，$M$の下界は$\emptyset$であり，これは下限でもある．
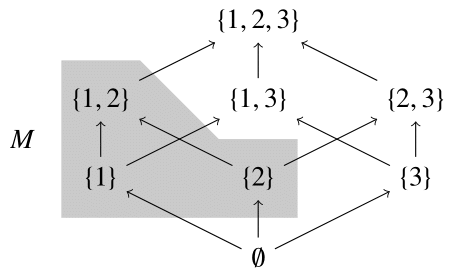
例 7.10
$P=\{a,b,c,d,e\}$に対し，順序集合$(P,\leq_P)$を次のハッセ図で定義する．
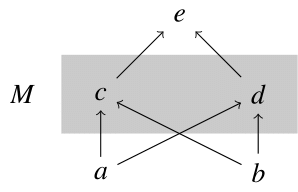$M=\{c,d\}$とすると，$M$の上界は$e$であり，上限は$e$である．一方，$M$の下界は$a$と$b$であり，下限は存在しない．
このように，
- 上界や下界が存在しても，上限や下限が存在するとは限らない
- 上限や下限は$M$の中にあるとは限らない
命題 7.11
$(P,\leq_P)$を順序集合，$M$を$P$の空でない部分集合とする．このとき，
-
$\sup (M) \in M \Rightarrow \sup (M) = \max (M)$，
-
$\inf (M) \in M \Rightarrow \inf (M) = \min (M)$．
証明
(1) $a=\sup(M)$とする．このとき定義から，任意の$x \in M$に対し，$x \leq_P a$が成り立つ．$a \in M$であるので，これは$a$が$M$の最大元であるという定義を満たす．
(2) (1)と同様．
これまでの例は全て有限集合であったが，無限集合で考えると，異なる状況が生じる．例えば，極大（小）元は無限集合の場合存在するとは限らない．
(2) (1)と同様．
例 7.12
$\mathbb{R}$を実数全体の集合とし，通常の不等号$\leq$を用いた順序集合$(\mathbb{R},\leq)$を考える．さらに，$\mathbb{R}$の部分集合として
\[
M= \left\{ x \in \mathbb{R} : 0 \leq x \lt \sqrt{2}\right\} \]
とする．このとき，$M$の最大元，最小元，上限，下限を求める．
数直線で考えると，$M$の上界全体の集合は$U(M)=\left\{ x\in \mathbb{R} : \sqrt{2} \leq x \right\}$である．特に，$M$の上限は$\sup(M)=\sqrt{2}$である．このとき，$M$の上限は$M$に属さない，つまり$\sup(M) \notin M$である． 一方，$M$の下界全体の集合は$L(M)=\{ x \in \mathbb{R} : x \leq 0\}$である．特に，$M$の下限は$\inf(M)=0$であり，$\inf(M) \in M$となっている．よって命題7.11より$M$の最小元は$\min(M)=\inf(M)=0$である．
$M$は極大元を持たない，特に最大元を持たないことを示す． $M$が極大元$a$を持ったとする．このとき，$a \lt \sqrt{2}$である．$0 \lt \sqrt{2}-a$であるので， \[ a \lt a + \frac{(\sqrt{2}-a)}{2} \lt a+ (\sqrt{2}-a) =\sqrt{2} \] が成り立つ．よって$b=a + \dfrac{(\sqrt{2}-a)}{2}$とすると，$b \in M$となることがわかる．しかし，これは$a$が$M$の極大元であることに矛盾する．よって$M$は極大元を持たない．
数直線で考えると，$M$の上界全体の集合は$U(M)=\left\{ x\in \mathbb{R} : \sqrt{2} \leq x \right\}$である．特に，$M$の上限は$\sup(M)=\sqrt{2}$である．このとき，$M$の上限は$M$に属さない，つまり$\sup(M) \notin M$である． 一方，$M$の下界全体の集合は$L(M)=\{ x \in \mathbb{R} : x \leq 0\}$である．特に，$M$の下限は$\inf(M)=0$であり，$\inf(M) \in M$となっている．よって命題7.11より$M$の最小元は$\min(M)=\inf(M)=0$である．
$M$は極大元を持たない，特に最大元を持たないことを示す． $M$が極大元$a$を持ったとする．このとき，$a \lt \sqrt{2}$である．$0 \lt \sqrt{2}-a$であるので， \[ a \lt a + \frac{(\sqrt{2}-a)}{2} \lt a+ (\sqrt{2}-a) =\sqrt{2} \] が成り立つ．よって$b=a + \dfrac{(\sqrt{2}-a)}{2}$とすると，$b \in M$となることがわかる．しかし，これは$a$が$M$の極大元であることに矛盾する．よって$M$は極大元を持たない．
例 7.13
$\mathbb{R}$を有理数全体の集合とし，通常の不等号$\leq$を用いた順序集合$(\mathbb{R},\leq)$を考える．さらに，$\mathbb{R}$の部分集合として
\[
M=\left\{ \frac{1}{n} : n \in \mathbb{N} \right\}
\]
とする．ここで，$\mathbb{N}$は自然数全体の集合である．
このとき，$M$の最大元，最小元，上限，下限を求める．
任意の自然数$n \in \mathbb{N}$に対し， \[ 0\lt \dfrac{1}{n} \leq \dfrac{1}{1}=1 \] なので， $M$の上界全体の集合は$U(M)=\{ x \in \mathbb{R} : 1 \leq x \}$である．特に，$M$の上限は$\sup(M)=1$である．このとき，$\sup(M) \in M$であるので，命題7.11より$M$の最大元は$\max(M)=\sup(M)=1$である．
一方，$M$の下界全体の集合は$L(M)=\{ x \in \mathbb{R} : x \leq 0\}$である．特に，$M$の下限は$\inf(M)=0$である．このとき，$\inf(M) \notin M$となっていることに注意する．
$M$は極小元をもたない，特に最小元を持たないことを示す． $M$が極小元$a$を持ったとする．$a\in M$であるので，ある自然数$n \in \mathbb{N}$を使って，$a=\frac{1}{n}$と書ける．このとき， \[ \dfrac{1}{n+1} \lt \dfrac{1}{n}=a \] が成り立ち，$\frac{1}{n+1} \in M$であるので，これは$a$が $M$の極小元であることに矛盾する．よって$M$は極小元を持たない．
任意の自然数$n \in \mathbb{N}$に対し， \[ 0\lt \dfrac{1}{n} \leq \dfrac{1}{1}=1 \] なので， $M$の上界全体の集合は$U(M)=\{ x \in \mathbb{R} : 1 \leq x \}$である．特に，$M$の上限は$\sup(M)=1$である．このとき，$\sup(M) \in M$であるので，命題7.11より$M$の最大元は$\max(M)=\sup(M)=1$である．
一方，$M$の下界全体の集合は$L(M)=\{ x \in \mathbb{R} : x \leq 0\}$である．特に，$M$の下限は$\inf(M)=0$である．このとき，$\inf(M) \notin M$となっていることに注意する．
$M$は極小元をもたない，特に最小元を持たないことを示す． $M$が極小元$a$を持ったとする．$a\in M$であるので，ある自然数$n \in \mathbb{N}$を使って，$a=\frac{1}{n}$と書ける．このとき， \[ \dfrac{1}{n+1} \lt \dfrac{1}{n}=a \] が成り立ち，$\frac{1}{n+1} \in M$であるので，これは$a$が $M$の極小元であることに矛盾する．よって$M$は極小元を持たない．
注意 7.14
極大（小）元は「境界（端）の点」というイメージであり，上記2つの例の極大（小）元を持たない証明は，点を適当にとったとき，それより遠い点が範囲内でとれ，さらにそれより遠い点が範囲内でとれ，⋯とこの操作が延々と繰り返されていつまで経っても境界（端）に辿りつかない，つまり境界（端）が存在しないということで証明している．