8回目：束
8.1 束
上限と下限は有限集合であったとしても，いつも存在するとは限らないことを見た． この節では，有限部分集合がいつでも上限と下限を持つような順序集合に着目して，その性質を調べる．定義 8.1
順序集合$(L,\leq_L)$が束 (lattice)であるとは，$L$の任意の空でない有限部分集合に対して，上限と下限が存在するときにいう．
例 8.2
$L=\{a,b,c,d\}$に対し，順序集合$(L,\leq_L)$を次のハッセ図で定義する．
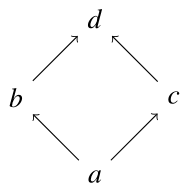このとき，$L$の1元からなる集合は自身を上限，下限に持ち，2元からなる集合，例えば，$\{a,b\}$なら，上限$b$，下限$a$を持ち，$\{b,c\}$なら上限$d$，下限$a$を持つ．この議論を続けると，すべての空でない有限部分集合は上限と下限を持つことがわかるので，$(L,\leq_L)$は束である．
例 8.3
$L=\{a,b,c,d\}$に対し，順序集合$(L,\leq_L)$を次のハッセ図で定義する．
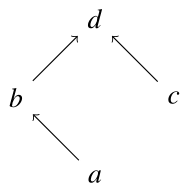このとき，$L$全体では上限$d$を持つが，下限は持たない．特に，２元からなる集合$\{a,c\}$も下限を持たない．よって$(L,\leq_L)$は束ではない．
順序集合が束であるためには，すべての空でない有限部分集合に対して，上限と下限の存在を確認しないといけないが，実は，2元からなる集合だけ確認すれば十分である．
定理 8.4
順序集合$(L,\leq_L)$が束となる必要十分条件は，$L$の任意の2元$x,y \in L$に対し，$\{x,y\}$が上限と下限を持つことである．
証明
$\Rightarrow$は束の定義から明らか．$\Leftarrow$を示す．
これは，任意の2元$x,y \in L$に対し，$\{x,y\}$が上限と下限を持てば，$L$の任意の空でない有限部分集合は上限と下限を持つことを示せばよい．
$L$の任意の空でない有限部分集合$M$をとり，$M$の元の個数$n$に関する帰納法で証明する．$n=1$のとき，$M=\{a_1\}$とすると，$a_1$は$M$の上限かつ下限である．
$n \geq 2$と仮定し，$M=\{a_1,\ldots,a_n\}$とする．
帰納法の仮定から$N=M \setminus \{a_n\}=\{a_1,\ldots,a_{n-1}\}
$は上限と下限を持つ．その上限を$\sup (N)=a$とする．このとき，$a_1,\ldots,a_{n-1} \leq_L a$である．仮定から，$\{a, a_{n}\}$は上限を持つので，それを$a'$とする．すると，$a, a_{n} \leq_L a'$が成り立つ．特に，
\[
a_1,\ldots,a_n \leq_L a'
\]
である．
よって$a'$は$M$の上界である．
$a'$が$M$の上限であることを示す．
$M$の任意の上界$u$をとる．このとき，$a_{n} \leq_L u$が成り立つ．また$a$は$N$の上限，つまり最小上界であり，$u$は$N$の上界でもあるので，$a \leq_L u$である．よって$u$は$\{a, a_{n}\}$の上界である．$a'$は$\{a, a_{n}\}$の上限であったので，$a' \leq_L u$が成り立つ．よって$a'$が$M$の最小上界であることがわかるので，$a'$は$M$の上限である．
$M$が下限を持つことも同様に証明できる．
8.2 結びと交わり
上限と下限はそれぞれ上界と下界の最大元と最小元であった．最大元と最小元は存在すれば唯一であったことを思い出そう．よって，もし$(L, \leq_P)$が束であれば，$L$の任意の2元$x,y \in L$に対し，$\{x,y\}$の上限，下限がただ1つ決まる．それを$x \vee y$と$x \wedge y$で表し，$x$と$y$の結び (join)と交わり (meet)と呼ぶ．つまり， \[ x \vee y:= \sup(\{x,y\}), \ \ \ \ \ \ x \wedge y := \inf(\{x,y\}) \] である． $x$と$y$が比較可能であれば$\vee$と$\wedge$を計算することは容易である．命題 8.5
$(L,\leq_L)$を束とし，$x,y \in L$とする．
このとき，次の3条件は同値である．
-
$x \leq_L y$，
-
$x \vee y= y$，
-
$x \wedge y = x$，
証明
(1) $\Rightarrow$ (2)を示す．
(1)より$y$は$\{x,y\}$の上界である．かってな$\{x,y\}$の上界$u$をとると，$y \leq_L u$が成り立つので，$y$は最小上界，つまり$\{x,y\}$の上限である．よって$x \vee y=y$である．
次に(2) $\Rightarrow$ (1)を示す．(2)より$y$は$\{x,y\}$の上限である．このとき，$y=\sup(\{x,y\}) \in \{x,y\}$であるので，前回の命題7.11より$y$は$\{x,y\}$の最大元である．よって$x \leq_L y$が成り立つ．
(1) $\Leftrightarrow$ (3)は同様に証明できる．
この$\vee$や$\wedge$は束$(L, \leq_L)$における和と積だと考える．
この演算に対し，以下の性質が成り立つ（証明は省略）．
定理 8.6
$(L, \leq_L)$を束とし，$x,y,z \in L$とする．このとき，次が成り立つ．
この性質を用いることで，上限や下限について計算ができる．例えば，
\[
( x \wedge \bot ) \vee (\top \wedge y) \overset{交換律}{=} (\bot \wedge x ) \vee ( \top \wedge y)\overset{最小元の性質}{=} \bot \vee (\top \wedge y) \overset{最小元の性質}{=} \top \wedge y \overset{最大元の性質}{=} y
\]
のように計算できる．
しかし，束の和と積の演算では，分配法則が成り立つとは限らない．ここで分配法則（分配律）とは，
- (交換律) $x \vee y = y \vee x$, $x \wedge y = y \wedge x$
- (結合律) $(x \vee y) \vee z = x \vee (y \vee z)$, $(x \wedge y) \wedge z = x \wedge (y \wedge z)$
- (冪等律) $x \vee x=x$, $x \wedge x =x$
- (吸収律) $x \wedge (x \vee y)=x$, $x \vee (x \wedge y)=x$
- (最大元の性質) $\top \wedge x =x$, $\top \vee x=\top $
- (最小元の性質)$\bot \wedge x=\bot$, $\bot \vee x = x$
- (分配律1) $x \vee (y \wedge z) = (x \vee y) \wedge (x \vee z )$
- (分配律2) $x \wedge (y \vee z) = (x \wedge y) \vee (x \wedge z )$
例 8.7
$L=\{a,b,c,\top,\bot\}$に対し，順序集合$(L,\leq_L)$を次のハッセ図で定義する．
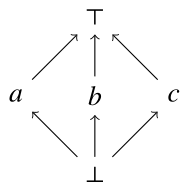$L$が束となることの確認は各自にまかせる．
このとき，
\[ a \vee b = b \vee c = a \vee c = \top\]
\[ a \wedge b = b \wedge c = a \wedge c = \bot\]
であるので，
\[
a \vee ( b \wedge c) = a \vee \bot = a \neq \top = \top \wedge \top = (a \vee b ) \wedge (a \vee c)
\]
であり，分配律が成り立たない$a,b,c \in L$が存在する．
8.3 分配束とモジュラー束
定義 8.8
束$(L,\leq_L)$は，任意の$x,y,z \in L$に対し，分配律が成り立つとき，分配束 (distributive lattice)と呼ばれる．
例 8.9
$X=\{1,2,3\}, L=2^X$とし包含関係による順序集合$(L, \subset)$を考える．
このとき，$(L,\subset)$は束である．
注意深く考えると，この束の和と積は，集合の和集合と積集合である．
つまり，$A,B \in L$に対し，
\[
A \vee B = A \cup B, \ \ \ \ \ A \wedge B = A \cap B
\]
である（これが記号として$\vee$と$\wedge$を使う理由でもある）．
集合の和と積は分配法則が成り立っていたことを思い出すと，$(L,\subset)$が分配束となることがわかる．
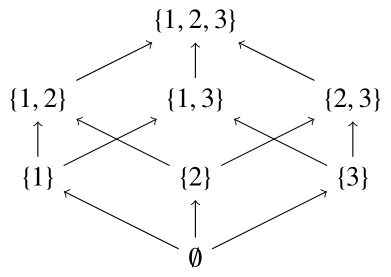
分配束は，集合の和集合や積集合の計算とほぼ同じ感覚で上限や下限の計算を行うことができる．
次に，もう1つ分配束とならない例を見てみよう．
例 8.10
$L=\{a,b,c,\top,\bot\}$に対し，順序集合$(L,\leq_L)$を次のハッセ図で定義する．
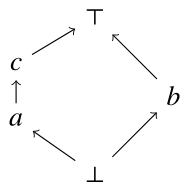$L$が束となることの確認は各自にまかせる．
このとき，
\[ a \vee b = b \vee c = \top\]
\[ a \wedge b = b \wedge c = \bot\]
であり，$a \vee c = c$かつ$a \wedge c=a$なので，
\[
a \vee ( b \wedge c) = a \vee \bot =a \neq c = \top \wedge c = (a \vee b ) \wedge (a \vee c)
\]
であり，分配律が成り立たない$a,b,c \in L$が存在する．よって$(L,\leq_P)$は分配束ではない．
実は，例8.7と8.10は分配束ではない本質的な束である．
束$(L,\leq_L)$と$L$の部分集合$M$に対し，任意の$a,b \in M$が$a \vee b, a \wedge b \in M$を満たしているとき，$(M,\leq_L)$を$(L,\leq_L)$の部分束 (sublattice)という．
例えば，下の束$\{\top,a,b,c,d, \bot\}$に対し，部分集合$\{\top,a,b,d,\bot\}$は部分束である．
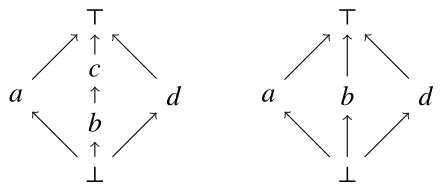
定理 8.11
束$(L,\leq_L)$が分配束となる必要十分条件は，$(L,\leq_L)$が
というハッセ図で表される部分束を持たないことである．
この結果により，分配束かどうかはハッセ図を書けば視覚的にある程度わかる．例えば，定理の直前の束とその部分束はともに分配束ではない．
さて，数の通常の演算において和と積の順番を入れ替えることはできない．例えば，$(1+2) \times 2 \neq 1+(2\times 2)$である．しかし，分配束$(L,\leq_L)$は次のような性質を持つ．$x,y,z \in L$に対し，
- (モジュラー律) $x \leq_L y \Rightarrow (x \vee z) \wedge y= x \vee (z \wedge y)$.
定義 8.12
束$(L,\leq_L)$は，任意の$x,y,z \in L$に対し，モジュラー律が成り立つとき，モジュラー束 (modular lattice)と呼ばれる．
定理 8.13
分配束はモジュラー束である．
証明
$(L, \leq_L)$をかってな分配束とし，任意の$x,y,z \in L$で，$x \leq_L y$となるものをとる．このとき，
\[
(x \vee z) \wedge y \overset{\mbox{分配律}}{=} (x \wedge y) \vee (z \wedge y) \overset{\mbox{命題8.5}}{=} x \vee (z \wedge y).
\]
よってモジュラー律が成り立つので，$(L,\leq_L)$はモジュラー束である．
この定理の逆は成り立たない．
実際，定理8.11と同じように，モジュラー束も特徴づけが知られており，それらを比べると例8.7はモジュラー束であるが，分配束ではないことがわかる．
定理 8.14
束$(L,\leq_L)$がモジュラー束となる必要十分条件は，$(L,\leq_L)$が
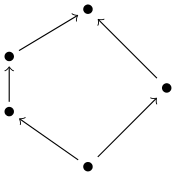というハッセ図で表される部分束を持たないことである．
例8.10がモジュラー束とならないことは，$a \leq_L c$であるが，
\[
(a \vee b) \wedge c =\top \wedge c=c \neq a = a \vee \bot = a \vee (b \wedge c)
\]
よりわかる．
束には他にも様々な興味深い性質がある，束を中心的に取り扱う理論を束理論と呼ぶ．