11回目:オイラー数
文字$1,2,\ldots,n$の順列$\pi=c_1 c_2 \cdots c_n$全体の集合を$\mathfrak{S}_n$とする.このとき$|\mathfrak{S}_n|=n!$である.順列$\pi=c_1 c_2 \cdots c_n \in \mathfrak{S}_n $の降下集合を \[ D(\pi):=\{ i : c_i > c_{i+1}\} \subset \{1,2,\ldots,n\} \] と定義する. 例えば,$n=7$と$\pi=3421576$ならば$D(\pi)=\{2,3,6\}$である. いま,整数$n\geq 1$と$0 \leq q \leq n-1$を固定し,順列$\pi \in \mathfrak{S}_n$で$|D(\pi)|=q$となるもの全体の集合を$A_{n,q}$で表す.つまり \[ A_{n,q}=\{\pi \in \mathfrak{S}_n : |D(\pi)|=q\} \] である.さらに$A_{n,q}$の元の個数を$a_{n,q}$で表し,これを$n$の$q$番目の\textbf{オイラー数}と呼ぶ.つまり \[ a_{n,q}=| A_{n,q}|\] である.例 11.1
$n=3$のとき,$\mathfrak{S}_3$は
\begin{align*}
123&& 132&& 213\\
231&&312&&321
\end{align*}
の6個からなる.すると
\[
A_{3,0}=\{123\}, A_{3,1}=\{132,213,231,312\}, A_{3,2}=\{321\}
\]
である.よって
\[
a_{3,0}=1, a_{3,1}=4,a_{3,2}=1
\]
である.
以下,$n$を固定し,$n$のオイラー数の数列$a_{n,0},a_{n,1},\ldots,a_{n,n-1}$を考える.
命題 11.2
数列$a_{n,0},a_{n,1},\ldots,a_{n,n-1}$は対称数列である.つまり,$a_{n,q}=a_{n,n-1-q}$が任意の$0 \leq q \leq n-1$で成り立つ.
証明
順列$\pi=c_1c_2 \cdots c_n$に対し順列$\pi^{*}=c_nc_{n-1} \cdots c_1$を考える.
いま$i \in D(\pi)$ (resp. $i \notin D(\pi)$)をとる.すると$c_i > c_{i+1}$ (resp. $c_i < c_{i+1}$)である.
このとき,順列
\[
\pi^{*}=c_n \cdots c_{i+1} c_i \cdots c_1\]
において,$c_{i+1}$は左から$(n+1)-(i+1)$であるから$(n+1)-(i+1) \notin D(\pi^*)$ (resp. $(n+1)-(i+1) \in D(\pi^*)$)である.
特に,\[i \in D(\pi) \Leftrightarrow (n+1)-(i+1) \notin D(\pi^*) \]が成り立つ.
したがって,$|D(\pi)|=q$であれば,
$|D(\pi^*)|=n-1-q$
である.
すると写像
\[
A_{n,q} \to A_{n,n-1-q}, \ \ \ \ \pi \mapsto \pi^*
\]
は全単射となるので$a_{n,q}=a_{n,n-1-q}$が成り立つ.
命題 11.3
任意の整数$n \geq 3$と$1 \leq q \leq n-2$に対して漸化式
\[
a_{n,q}=(n-q)\cdot a_{n-1,q-1} + (q+1) \cdot a_{n-1,q}
\]
が成立する.
証明の前にこの命題を意味を述べると,以下のように$a_{1,0}$から順に$a_{n,q}$が計算できるということである.
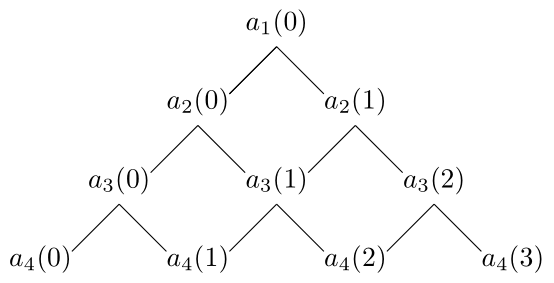
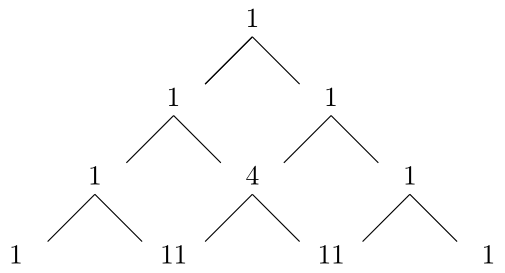
証明
文字$1,2,\ldots,n$の順列$\pi$は$1,2,\ldots,n-1$の順列$\sigma=c_1 c_2 \cdots c_{n-1}$のある$c_i$と$c_{i+1}$の間に$n$を入れることで作ることができる.ただし,$i=0$のときは$c_1$の前に$n$を置くこととし,$i=n-1$のときは$c_{n-1}$の後ろに$n$を置くこととする.いま$c_i\lt c_{i+1}$であるとすると,$c_i \lt n > c_{i+1}$であるから$D(\pi)$の元の個数は$D(\sigma)$の元の個数よりちょうど$1$だけ大きくなる.
一方,$c_i > c_{i+1}$とすると,$c_i \lt n > c_{i+1}$であるから,$D(\sigma)$の元の個数と$D(\pi)$の元の個数は一致する.ただし,$n$を$c_1$の前に置くときは前者に含まれ,$n$を$c_{n-1}$の後ろに置くときは後者に含まれる.
すると文字$1,2,\ldots,n$の順列$\pi$で$| D(\pi)|=q$となるものは
次にオイラー数の数列が実根,特に単峰となることを示そう.
これは多項式$\sum_{q=0}^{n-1}a_{n,q}x^q$が実零点のみを持つということだが,これは$n$次多項式
\[
f_n(x)=x\sum_{q=0}^{n-1}a_{n,q}x^q=\sum_{q=1}^n a_{n,q-1} x^q
\]
が実零点のみを持つことと同値である.こちらを示す.漸化式と具体的な計算により以下の補題が成り立つ.
- (i) 文字$1,2,\ldots,n-1$の順列$\sigma=c_1 c_2 \cdots c_{n-1}$で$| D(\sigma)|=q-1$となるものから$c_i \lt c_{i+1}$を満たす文字の間に$n$を入れたもの
- (ii) 文字$1,2,\ldots,n-1$の順列$\sigma=c_1 c_2 \cdots c_{n-1}$で$| D(\sigma)|=q$となるものから$c_i > c_{i+1}$を満たす文字の間に$n$を入れたもの
補題 11.4
$f_1(x)=x$かつ任意の$n=2,3,4,\ldots$に対し,
\[
f_n(x)=(x-x^2) f'_{n-1}(x)+nx f_{n-1}(x)
\]
が成り立つ.
次に
\[
g_n(x)=\frac{f_n(x)}{(x-1)^{n+1}}
\]
とおく.先ほどの補題を使うと次の補題が証明できる.
補題 11.5
$g_n(x)=-xg'_{n-1}(x)$
が成り立つ.
以上の準備の下,次の定理を証明する.
定理 11.6
数列$a_{n,0},a_{n,1},\ldots,a_{n,n-1}$は実根数列,特に単峰である.
証明
まず$g_n(x)=0$が$x \lt 1$の範囲において重複を込めて$n$個の解を持つことを示す.まず$n=1$とすると
\[
g_1(x)=\frac{f_1(x)}{(x-1)^2}=\frac{x}{(x-1)^2}
\]
だから$n=1$のときは成立する.
$n$に関する帰納法で示すために,$n \geq 2$とし,$n-1$までは正しいとする. すると$g_{n-1}(x)=0$は$x\lt 1$の範囲で重複を込めて$n-1$個の解を持つ. その解のうち最小のものと$\delta$とする.このとき補題10.3と補題10.4の証明から$g'_{n-1}(x)=0$は$\delta \leq x \lt 1$の範囲で重複を込めて少なくとも$n-2$個の解を持つ.ところが$f_{n-1}(x)$は$n-1$次多項式であるから$\lim\limits_{x \to -\infty}g_{n-1}(x)=0$である.したがって$g'_{n-1}(x)=0$は$x \lt \delta$の範囲で少なくとも1つの解を持つ.すると補題11.5から$g_{n}(x)=0$は$x \lt 1$の範囲で少なくとも$n$個の解をもつ.特に$n$次多項式$f_n(x)$は$x\lt 1$の範囲で$n$個の解を持つことになり,数列$a_{n,0},a_{n,1},\ldots,a_{n,n-1}$は実根数列となることがわかった.
$n$に関する帰納法で示すために,$n \geq 2$とし,$n-1$までは正しいとする. すると$g_{n-1}(x)=0$は$x\lt 1$の範囲で重複を込めて$n-1$個の解を持つ. その解のうち最小のものと$\delta$とする.このとき補題10.3と補題10.4の証明から$g'_{n-1}(x)=0$は$\delta \leq x \lt 1$の範囲で重複を込めて少なくとも$n-2$個の解を持つ.ところが$f_{n-1}(x)$は$n-1$次多項式であるから$\lim\limits_{x \to -\infty}g_{n-1}(x)=0$である.したがって$g'_{n-1}(x)=0$は$x \lt \delta$の範囲で少なくとも1つの解を持つ.すると補題11.5から$g_{n}(x)=0$は$x \lt 1$の範囲で少なくとも$n$個の解をもつ.特に$n$次多項式$f_n(x)$は$x\lt 1$の範囲で$n$個の解を持つことになり,数列$a_{n,0},a_{n,1},\ldots,a_{n,n-1}$は実根数列となることがわかった.