3.4：有限群
定義 3.11
$G$を群とする．もし$G$が有限集合なら$G$を有限群という．またこのとき，$|G|$を$G$の位数という．$G$が無限集合のときは$G$を無限群という．
$G$が有限群の場合，$a \circ b$の計算結果を表にした乗法表（積表）を書くと便利である．つまり，以下のような表である．
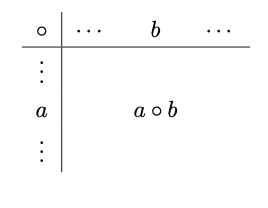
例 3.12
1元集合$G=\{e\}$を考える．このとき$G$上の演算$\circ$（で表される式）は$e \circ e = e$しかない．つまり，乗法表は以下のようになる．
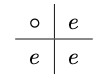このとき，$(G,\circ)$は群となる（確かめよ）．このような1元からなる群を自明群という．
例 3.13
自明群の次に単純な群を見ていく．つまり，$G=\{e,g\}$という2元集合とその演算$\circ$を考える．$e$を単位元とすると，$e \circ g = g \circ e=g$と$e \circ e=e$は自動的に決まる．よって$g \circ g=e$または$g \circ g =g$となるが，$g$に逆元が存在しないといけないので，$g \circ g=e$となる．よって演算$\circ$の対応が自動的に決まった．実際，乗法表は以下の通りとなる．
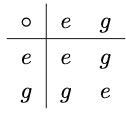したがって，位数$2$の有限群は「本質的には」この群しかない．
実は位数$3$の有限群も本質的には1つしかない．
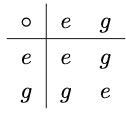
例 3.14
$G=\{e,g,h\}$という3元集合とその演算$\circ$を考える．$e$を単位元とする．逆元の一意性から乗法表の各行および各列にはちょうど1個$e$が入らなければならない．よってもし$g^2=e$ならば$h^2=e$となる（下図参照）．
しかし，単位元の一意性から$g \circ h \neq g,h$であるので，乗法表が定まらない．したがって，$G$の乗法表の可能性は以下の1通りのみである．
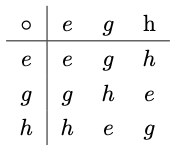したがって，位数$3$の有限群は「本質的には」この群しかない．
位数$4$で「本質的に」異なる有限群が現れる．
例 3.15
$G=\{e,a,b,c\}$という4元集合とその演算$\circ$を考える．$e$を単位元とすると．$G$の乗法表は「本質的には」以下の2種類が存在する（$\circ_1$と$\circ_2$で分けて書く）．
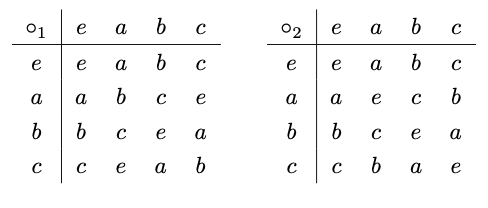違いがわかりにくいかもしれないが，右の表だと$a^2=b^2=c^2=e^2=e$となっているが，左の表は$a^2 \neq e$である．よってこの2つの乗法表で定義される群$(G,\circ_1)$と$(G,\circ_2)$は「本質的には」違う有限群である．
「本質的には」同じ群や違う群と表現しているが，この意味は後の章で説明する．
次に代表的な有限アーベル群の例を紹介する．
$m$を$2$以上の自然数とし，$\mathbb{Z}/m\mathbb{Z}$上の演算$+$を以下で定義する．
$+:$
$\mathbb{Z}/m\mathbb{Z} \times \mathbb{Z}/m\mathbb{Z} $
$\longrightarrow$
$\mathbb{Z}/m\mathbb{Z}$
$\in$
$\in$
$(\overline{a},\overline{b})$
$\longmapsto$
$\overline{a}+\overline{b}:=\overline{a+_{\mathbb{Z}}b}$
命題 3.16
$\mathbb{Z}/m\mathbb{Z}$上の演算$+$はwell-definedである．
証明
示すべきことは，任意の剰余類$\overline{a}=\overline{a'}$と$\overline{b}=\overline{b'}$に対し，$\overline{a}+\overline{b}=\overline{a'}+\overline{b'}$が成り立つことである．
$+$の定義から$\overline{a}+\overline{b}=\overline{a+b}$かつ$\overline{a'}+\overline{b'}=\overline{a'+b'}$である．仮定から$a \equiv_m a'$かつ$b \equiv_m b'$であるので，この両片を足すと$a+b \equiv_m a'+b'$が得られる．これは$\overline{a+b}=\overline{a'+b'}$を意味するので．$\overline{a}+\overline{b}=\overline{a'}+\overline{b'}$が成り立つ．よって$+$はwell-definedである．
それではこの演算に対して$\mathbb{Z}/m\mathbb{Z}$がアーベル群であることを見る．
命題 3.17
$(\mathbb{Z}/m\mathbb{Z},+)$は有限アーベル群である．またその位数は$m$である．
証明
(G1) 任意の$\overline{a},\overline{b},\overline{c}\in \mathbb{Z}/m\mathbb{Z}$に対し，
\[
(\overline{a}+\overline{b})+\overline{c}=\overline{a+b}+\overline{c}=\overline{(a+b)+c}=\overline{a+(b+c)}=\overline{a}+(\overline{b+c})=\overline{a}+(\overline{b}+\overline{c})
\]
より結合律が成り立つ．
(G2) $e=\overline{0}$とすると，任意の$\overline{a} \in \mathbb{Z}/m\mathbb{Z}$に対し， \[ \overline{a}+\overline{0}=\overline{a+0}=\overline{a}=\overline{0+a}=\overline{0}+\overline{a} \] なので，単位元が存在する．
(G3) 任意の$\overline{a} \in \mathbb{Z}/m\mathbb{Z}$に対し，$\overline{-a}$を考えると， \[ \overline{a}+\overline{-a}=\overline{a+(-a)}=\overline{0}=\overline{(-a)+a}=\overline{-a}+\overline{a} \] なので，逆元が存在する．
(G4) 任意の$\overline{a},\overline{b} \in \mathbb{Z}/m\mathbb{Z}$に対し， \[ \overline{a}+\overline{b}=\overline{a+b}=\overline{b+a}=\overline{b}+\overline{a} \] であるので交換律が成り立つ．
また$|\mathbb{Z}/m\mathbb{Z}|=m$であるので，以上より$(\mathbb{Z}/m\mathbb{Z},+)$は位数$m$の 有限アーベル群である．
以降，断りがない限り，$\mathbb{Z}/m\mathbb{Z}$で群$(\mathbb{Z}/m\mathbb{Z},+)$を意味する．
\bigskip
次に$(\mathbb{Z}/m\mathbb{Z})^{\times}$を考える．$\mathbb{Z}/m\mathbb{Z}$と同様に$+$が定義できそうだが実はできない．実際，$m=3$とすると，$(\mathbb{Z}/3\mathbb{Z})^{\times}=\{\overline{1},\overline{2}\}$であるが，$\overline{1}+\overline{2}=\overline{0} \notin (\mathbb{Z}/m\mathbb{Z})^{\times}$となる．つまり，演算の結果が同じ集合に属さないのである．演算の結果がいつでも同じ集合に属するのもwell-defined性では必要となる．
そこで，演算$\cdot$を考える．
$(\mathbb{Z}/m\mathbb{Z})^{\times}$上の演算$\cdot$を以下で定義する．
(G2) $e=\overline{0}$とすると，任意の$\overline{a} \in \mathbb{Z}/m\mathbb{Z}$に対し， \[ \overline{a}+\overline{0}=\overline{a+0}=\overline{a}=\overline{0+a}=\overline{0}+\overline{a} \] なので，単位元が存在する．
(G3) 任意の$\overline{a} \in \mathbb{Z}/m\mathbb{Z}$に対し，$\overline{-a}$を考えると， \[ \overline{a}+\overline{-a}=\overline{a+(-a)}=\overline{0}=\overline{(-a)+a}=\overline{-a}+\overline{a} \] なので，逆元が存在する．
(G4) 任意の$\overline{a},\overline{b} \in \mathbb{Z}/m\mathbb{Z}$に対し， \[ \overline{a}+\overline{b}=\overline{a+b}=\overline{b+a}=\overline{b}+\overline{a} \] であるので交換律が成り立つ．
また$|\mathbb{Z}/m\mathbb{Z}|=m$であるので，以上より$(\mathbb{Z}/m\mathbb{Z},+)$は位数$m$の 有限アーベル群である．
$\cdot:$
$(\mathbb{Z}/m\mathbb{Z})^{\times} \times (\mathbb{Z}/m\mathbb{Z})^{\times} $
$\longrightarrow$
$(\mathbb{Z}/m\mathbb{Z})^{\times}$
$\in$
$\in$
$(\overline{a},\overline{b})$
$\longmapsto$
$\overline{a} \cdot \overline{b}:=\overline{a\cdot_{\mathbb{Z}} b}$
命題 3.18
$(\mathbb{Z}/m\mathbb{Z})^{\times}$上の演算$\cdot$はwell-definedである．
証明
$\overline{a},\overline{b} \in (\mathbb{Z}/m\mathbb{Z})^{\times}$に対して$\overline{a} \cdot \overline{b}=\overline{a \cdot b}$が$(\mathbb{Z}/m\mathbb{Z})^{\times}$に属することを示す．
これは$a \cdot b$と$m$が互いに素であることを意味する．これは$a$と$m$が互いに素かつ$b$と$m$が互いに素であることから従う．
よって$\overline{a} \cdot \overline{b} \in (\mathbb{Z}/m\mathbb{Z})^{\times}$である．
次に任意の既約剰余類$\overline{a}=\overline{a'}$と$\overline{b}=\overline{b'}$に対し，$\overline{a}\cdot\overline{b}=\overline{a'}\cdot\overline{b'}$が成り立つことを示す．
$\cdot$の定義から$\overline{a}\cdot\overline{b}=\overline{a\cdot b}$かつ$\overline{a'}\cdot \overline{b'}=\overline{a'\cdot b'}$である．仮定から$a \equiv_m a'$かつ$b \equiv_m b'$であるので，この両片を掛けると$a \cdot b \equiv_m a' \cdot b'$が得られる．これは$\overline{a \cdot b}=\overline{a' \cdot b'}$を意味するので．$\overline{a}\cdot \overline{b}=\overline{a'}\cdot \overline{b'}$が成り立つ．
以上より$\cdot$はwell-definedである．
命題 3.19
$((\mathbb{Z}/m\mathbb{Z})^{\times},\cdot)$は有限アーベル群である．またその位数は$\phi(m)$である．
証明
(G1), (G2), (G4)の証明は演習問題とする．ここで単位元は$\overline{1}$である．
(G3) 任意の$\overline{a} \in (\mathbb{Z}/m\mathbb{Z})^{\times}$をとる． このとき，$\gcd(a,m)=1$であるので，$ax+my=1$を満たす整数$x,y$が存在する．この$x$に対し，$\gcd(x,m)=1$である．実際，$\gcd(x,m) =:d\geq 2$だと，$ax+my=1$の左辺が$d$の倍数となり，右辺が$1$なので矛盾である．したがって$\overline{x} \in (\mathbb{Z}/m\mathbb{Z})^{\times}$である．特に，$ ax \equiv_m 1 $であるので，$\overline{a} \cdot \overline{x}=\overline{ax}=\overline{1}$となることから，$\overline{x}$は$\overline{a}$の逆元である．
また$|(\mathbb{Z}/m\mathbb{Z})^{\times}|=\phi(m)$であるので，以上より$((\mathbb{Z}/m\mathbb{Z})^{\times},\cdot)$は位数$\phi(m)$の 有限アーベル群である．
以降，断りがない限り，$(\mathbb{Z}/m\mathbb{Z})^{\times}$で群$((\mathbb{Z}/m\mathbb{Z})^{\times},\cdot)$を意味する．
(G3) 任意の$\overline{a} \in (\mathbb{Z}/m\mathbb{Z})^{\times}$をとる． このとき，$\gcd(a,m)=1$であるので，$ax+my=1$を満たす整数$x,y$が存在する．この$x$に対し，$\gcd(x,m)=1$である．実際，$\gcd(x,m) =:d\geq 2$だと，$ax+my=1$の左辺が$d$の倍数となり，右辺が$1$なので矛盾である．したがって$\overline{x} \in (\mathbb{Z}/m\mathbb{Z})^{\times}$である．特に，$ ax \equiv_m 1 $であるので，$\overline{a} \cdot \overline{x}=\overline{ax}=\overline{1}$となることから，$\overline{x}$は$\overline{a}$の逆元である．
また$|(\mathbb{Z}/m\mathbb{Z})^{\times}|=\phi(m)$であるので，以上より$((\mathbb{Z}/m\mathbb{Z})^{\times},\cdot)$は位数$\phi(m)$の 有限アーベル群である．