7回目:格子凸多面体の代数幾何
格子凸多面体の研究で欠かせないのが代数幾何学との繋がりである.この節では詳しい定義は適宜飛ばし,雰囲気を感じ取ってほしい.定義 7.1
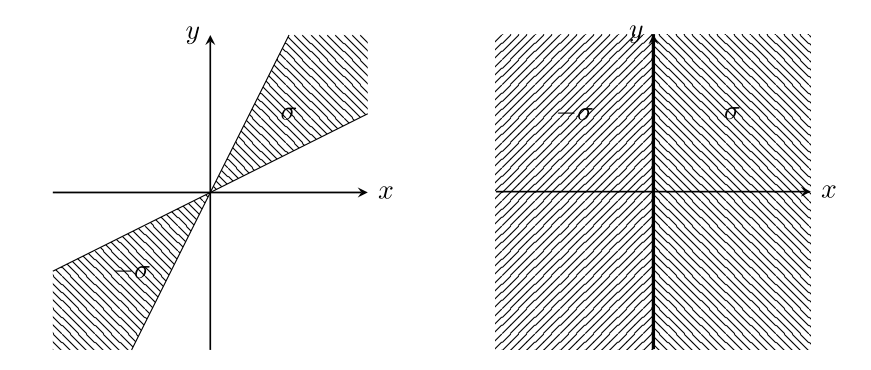
空間$\mathbb{R}^d$の集合$\sigma$が(多面)錐 (polyhedral cone)であるとは,有限個の点$\mathbf{v}_1,\mathbf{v}_2,\ldots,\mathbf{v}_s \in \mathbb{R}^d$が存在して,
\[
\sigma={\rm Cone}(\mathbf{v}_1,\ldots,\mathbf{v}_s):=\{a_1 \mathbf{v}_1+ \cdots + a_s \mathbf{v}_s : a_i \geq 0\}
\]
となるときにいう.また$\mathbf{v}_1,\ldots,\mathbf{v}_s$が全て格子点としてとれるとき,$\sigma$を有理凸錐という.さらに$\sigma \cap (-\sigma)=\{\mathbf{0}\}$のとき,$\sigma$を強凸錐と呼ぶ.ここで,$-\sigma={\rm Cone}(-\mathbf{v}_1,\ldots,-\mathbf{v}_s)$である.空集合$\emptyset$と${\rm Cone}(\emptyset)=\{\mathbf{0}\}$も有理強凸錐であるとする.アフィン空間${\rm aff}(\sigma)$の次元を$\sigma$の次元と定義する.
$d$次元有理強凸錐から$d$次元アフィントーリック多様体を構成することができる. したがってトーリック多様体を組合せ論的に捉えるには有理強凸錐が``うまく"貼り合わせられている集合を考えればいいと想像できるであろう. 凸多面体と同様で,錐$\sigma \subset \mathbb{R}^d$に対し,支持超平面を定義し,その共通部分を$\sigma$の面と呼ぶ.
定義 7.2
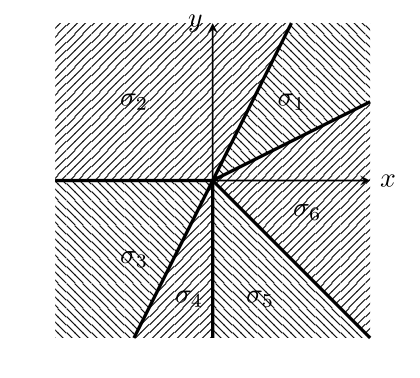
空間$\mathbb{R}^d$の扇 (fan) $\Sigma$とは有限個の有理強凸錐$\sigma \subset \mathbb{R}^d$の集合で,以下の条件を満たすもののことをいう:
任意の$\sigma \in \Sigma$に対し,$\sigma$の各面もまた$\Sigma$に属する.
任意の$\sigma_1,\sigma_2 \in \Sigma$に対し,その共通部分$\sigma_1 \cap \sigma_2$はそれぞれの面となっている.
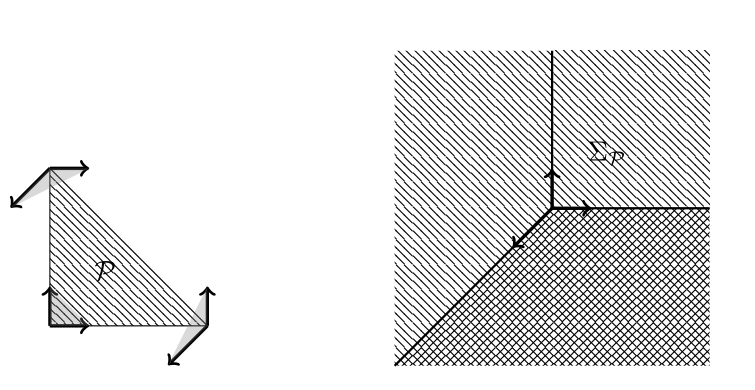
それではこのトーリック多様体と格子凸多面体の関係は何であろうか.まずは格子凸多面体から扇を構成する.$\mathcal{P} \subset \mathbb{R}^d$を$d$次元格子凸多面体とする.このとき$\mathcal{P}$は一意的なファセット表現 \[ \mathcal{P} = \{ \mathbf{x} \in \mathbb{R}^d : \mbox{任意の$\mathcal{P}$のファセット$\mathcal{F}$に対し$\langle \mathbf{a}_{\mathcal{F}}, \mathbf{x} \rangle \geq - b_{\mathcal{F}}$} \} \] を持つ.ここで$\mathbf{a}_{\mathcal{F}} \in \mathbb{Z}^d$と$b_{\mathcal{F}} \in \mathbb{Z}$は$b_{\mathcal{F}}=0$ならば$\mathbf{a}_{\mathcal{F}}$は原始的,つまり成分全体の最大公約数が$1$であり,そうでなければ$\mathbf{a}_{\mathcal{F}} / b_{\mathcal{F}} \notin \mathbb{Z}^d$を満たすものである. いま,$\mathcal{P}$の各面$\mathcal{Q}$に対し,有理強凸錐$\sigma_{\mathcal{Q}}$を \[ \sigma_{\mathcal{Q}}:={\rm Cone}( \mathbf{a}_F : \mathcal{F}\mbox{は$\mathcal{Q} \subset \mathcal{F}$となる$\mathcal{P}$のファセット}) \] で定義し, \[ \Sigma_{\mathcal{P}}:=\{ \sigma_{\mathcal{Q}} : \mathcal{Q}\mbox{は$\mathcal{P}$の面}\} \] で定義すると$\Sigma_{\mathcal{P}}$は扇となる.この扇を$\mathcal{P}$の正規扇 (normal fan)と呼び,対応するトーリック多様体を$\Sigma_{\mathcal{P}}$と書く.
定理 7.3
$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し,$X_{\mathcal{P}}$は$d$次元かつ射影的,つまり$X_{\mathcal{P}}$はある射影空間$\mathbb{P}^n$のZariski閉部分多様体として埋め込める.またどんな$d$次元射影トーリック多様体も$d$次元格子凸多面体から構成することができる.
したがって,射影トーリック多様体を調べたい場合,格子凸多面体を調べればいいことがわかる.しかし,一般に射影トーリック多様体と格子凸多面体は1対1ではない.例えば,格子凸多面体を膨らましてもその正規扇は変化しない.つまり凸多面体としては変化しているが,射影トーリック多様体は変化しないのである.これは一般に射影多様体は射影空間に埋め込めるかどうかだけを見ており,埋め込み方は気にしていないからである.射影トーリック多様体を研究するのであればこれで十分だが,格子凸多面体をより詳しく使うために,その埋め込み方も意識していく.
複素射影多様体$X$と$X$上の豊富な直線束$L$の組$(X,L)$は偏極多様体と呼ばれる(豊富な直線束の代わりに$X$上の豊富な因子$D$を用いて$(X,D)$を偏極多様体とすることもある). 詳しい定義は書かないが,この$L$や$D$が射影多様体の埋め込み方を表している.つまり,偏極多様体とは埋め込み方の情報も含んだ射影多様体である. 実は$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{R}^d$は上記のファセット表記を使って豊富な直線束$L_{\mathcal{P}}$を構成することができ,逆に$d$次元偏極トーリック多様体$(X,L)$からある$d$次元格子凸多面体$\mathcal{P}_{L}\subset \mathbb{R}^d$を構成することができる. この2つの構成方法により,1対1対応 \[ \{ (X,L) : \mbox{$d$次元偏極トーリック多様体}\} \overset{1:1}{\longleftrightarrow} \{\mathcal{P} \subset \mathbb{R}^d : \mbox{$d$次元格子凸多面体}\} \] を得る.
$\mathcal{P} \subset \mathbb{R}^d$を$d$次元格子凸多面体とし,$(X,L)$を対応する偏極トーリック多様体とすると,$\mathcal{P}$の体積やEhrhart多項式は次のような関係がある.
この他にも様々な代数幾何学の性質が格子凸多面体の言葉で翻訳されている(例えば非特異性やFano性など).今回は種数に関するある性質と格子凸多面体の数え上げの繋がりを紹介する. まず格子凸多面体の数え上げに関する有名な結果に日比の下限定理というものがある.
定理 7.4 (日比の下限定理)
$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{R}^d$が内部に格子点を持ったとする.つまり,$h^*_d \neq 0$である.このとき,任意の$2 \leq i \leq d-1$に対し,$h^*_1 \leq h^*_i$が成り立つ.
特に,内部に格子点を持てば,$h^*$列の全ての成分は正となることがわかる.
この定理は組合せ論的な手法で証明されている.そこで気になるのは,この定理が偏極トーリック多様体に対してはどういった意味を持つのかである.この定理が発表されて20年以上経った現在,この不等式の等号を満たす偏極トーリック多様体は特別なものになることが発見された.
定理 7.5 (川口)
$\mathcal{P} \subset \mathbb{R}^d$を内部に格子点を持つ$d$次元格子凸多面体とする.
このとき任意の$2 \leq i \leq d-1$に対し,$h^*_1=h^*_i$が成り立つことと対応する偏極トーリック多様体がCastelnuovoとなることは同値である.
この定理の理解するために次はCastelnuovo多様体とは何か見ていく.
古典的な代数幾何学における結果として,射影空間内の曲線に関する種数の上限が知られている.
定理 7.6 (Castelnuovo)
$C \subset \mathbb{P}^N$を種数$g$,次数$d$とする非退化な既約曲線とする.このとき,
\[
g \leq m (d-N) - \dfrac{1}{2}m(m-1)(N-1)
\]
が成り立つ.ただし,$m=\lfloor (d-1)/(N-1)\rfloor$である.
この種数の上限はCastelnuovo boundと呼ばれ,この上限に達する曲線のことをCastelnuovo曲線と呼ぶ.藤田はこのCastelnuovo曲線の高次元版を定義し,その性質を調べた.
$(X,L)$を$d$次元偏極多様体としたとき,$\chi(nL)$は$n$に関する$d$次多項式であり,$\chi_j(X,L)$を \[\chi(nL)=\sum_{j=0}^{d}\chi_j(X,L)\binom{n+j-1}{j}\] と定める. ここで$\chi_j(X,L) \in \mathbb{Z}$である. このとき,断面種数$g(X,L)$は次の式で定義される: \[ g(X,L):=1-\chi_{d-1}(X,L). \] 断面種数は偏極多様体の分類理論において重要な不変量である. 藤田はCastelnuovo boundの高次元版として,断面種数の上限を与えた.
定理 7.7 (藤田の上限定理)
$X$を$d$次元複素射影的多様体,$L$を$h^0(L) \geq d+2$を満たす$X$上の豊富な直線束とする.さらに,次の条件を仮定する:
このとき,
\[
g(X,L) \leq m \Delta(X,L) - \dfrac{1}{2}m(m-1)(L^d-\Delta(X,L)-1)
\]
が成り立つ.ただし,$m=\lfloor (L^d-1) /(L^d - \Delta (X,L)-1) \rfloor$かつ$\Delta(X,L)=L^d+d-h^0(L)$である.$\Delta(X,L)$は$(X,L)$の$\Delta$種数と呼ばれている.
定理 7.7の条件(2)の双有理性は上限を得るために必要不可欠である.
偏極多様体がCastelnuovoであるとは定理 7.7の仮定を満たし,かつその断面種数がこの上限に達するときにいう.
ここまでかなりの未定義語句が出てきたため,想像しにくくなっていると思うが,Castelnuovo多様体とは定理 7.7の意味で,断面種数が最大のものをいう.
この定理自体は格子凸多面体の言葉で言い換え可能である.
定義 7.8
$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{Z}^d$がspanningであるとは,
\[
\mathbb{Z} (( \mathcal{P} \cap \mathbb{Z}^d) \times \{1\} )= \mathbb{Z}^{d+1}
\]
が成立するときにいう.
ただし,有限集合$A=\{\mathbf{a}_1,\ldots,\mathbf{a}_r\} \subset \mathbb{Z}^d$に対し,$\mathbb{Z} A= \{ \lambda_ 1 \mathbf{a}_1+\cdots+\lambda_r \mathbf{a}_r : \lambda_1,\ldots,\lambda_r \in \mathbb{Z}\}$である.
つまり,$\mathcal{P}$がspanningであることと,$\mathbb{Z}^d$の任意の格子点が$\mathcal{P}$に含まれる格子点のアフィン整数結合で書けることと同値である.
命題 7.9
$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{R}^d$と対応する偏極トーリック多様体$(X,L)$に対して次が成り立つ:
$L$はbasepoint freeである.
$|L|$によって定まる射がその像に双有理であることと,$\mathcal{P}$がspanningであることは同値である.
$g(X,L)=h^*_2+2 h^*_3+\cdots (d-1) h^*_d$.
$\Delta(X,L)=h^*_2+h^*_3+\cdots+ h^*_d$.
したがって定理 7.7の格子凸多面体版は次のようになる.
定理 7.10
$\mathcal{P} \subset \mathbb{R}^d$を$d$次元格子凸多面体で$h^*_1 \geq 1$とする.
さらに$\mathcal{P}$はspanningであると仮定する.
このとき,
\begin{equation}
\label{eq:castel}
h^*_2+2h^*_3+\cdots+(d-1)h^*_{d} \leq m (h_2^*+\cdots+h^*_d)-\frac{m(m-1)}{2}h^*_1\cdots\cdots (7)
\end{equation}
が成り立つ.ただし,$m=\lfloor (h^*_1+\cdots+h^*_d)/h_1^* \rfloor$である.
$d$次元格子凸多面体$\mathcal{P}$が定理 7.10の仮定を満たし,さらに不等式(7)が等号となるとき,$\mathcal{P}$をCastelnuovo多面体と呼ぶ.つまり付随する偏極トーリック多様体がCastelnuovoとなる格子凸多面体である.したがって定理 7.5は内部に格子点を持つCastelnuovo多面体の特徴付けである.ではこの結果を拡張し,内部に格子点を持つとは限らないCastelnuovo多面体を特徴付けることは可能か.そのためには,日比の下限定理をまず拡張する必要がある.
定理 7.11 (Hofscheier-Katthän-Nill)
$\mathcal{P} \subset \mathbb{R}^d$を$d$次元spanning多面体とする.このとき,任意の$2 \leq i \leq \deg(\mathcal{P})-1$に対し,$h_1^* \leq h^*_{i}$が成り立つ.
それでは,一般のCastelnuovo多面体の特徴づけを紹介する.
定理 7.12 (土谷)
$\mathcal{P} \subset \mathbb{R}^d$を$d$次元格子凸多面体とする.
このとき$\mathcal{P}$がCastelnuovoになることと,次の3つの条件が成り立つことは同値である:
内部に格子点を持つ場合と違い定理 7.12の(1)と(3)の条件は必要である.
例 7.13
$\mathcal{P} \subset \mathbb{R}^4$を
\[
(0,0,0,0),(1,0,0,0),(0,1,0,0),(0,0,1,0),(1,1,0,2),(1,0,-1,0)
\]
を頂点とする$4$次元格子凸多面体とする.
このとき,$h^*(\mathcal{P})=(1,1,1,1,0)$である.つまり定理 7.12の(2)と(3)の条件を満たしている.一方で$(0,0,0,1) \in \mathbb{Z}^4$という格子点は$\mathcal{P} \cap \mathbb{Z}^4$のアフィン整数結合で書くことができないため,$\mathcal{P}$はspanningではない.したがって,定理 7.12より$\mathcal{P}$はCastelnuovoではない.
例 7.14
$\mathcal{P} \subset \mathbb{R}^3$を
\[
(0,0,0),(1,0,0),(0,1,0),(1,2,3),(0,0,-1)
\]
を頂点とする$3$次元格子凸多面体とする.
このとき,$h^*(\mathcal{P})=(1,1,2,0)$である.さらに$\mathcal{P}$がspanningであることも容易にわかる.よって定理 7.12の(1)と(2)の条件を満たしている.しかし(3)の条件を満たしていないため,$\mathcal{P}$はCastelnuovoではない.
補足 7.15
定理 7.12と定理 7.5を比べると内部に格子点を持てば,条件(1)と(3)が必要ではなくなる.条件(3)は簡単で,$\mathcal{P}$が内部に格子点を持てば,その条件は$|\mathcal{P} \cap \mathbb{Z}^d| \geq |{\rm int}(\mathcal{P}) \cap \mathbb{Z}^d|+(d+1)$であり,$\mathcal{P} \cap \mathbb{Z}^d$には少なくとも頂点($d+1$個以上)と内部の格子点が含まれるため,その不等式は成り立つ.
次に条件(1)だが,これは日比の下限定理の証明を見れば,内部に格子点を持ち条件(2)を満たすと(1)が成り立つことが証明できる.