3回目:数学の論理
3.1 命題
定義
文のうち,意味が明確であって,正しいかそうでないかが定まっている文のことを命題 (proposition)と呼ぶ.
命題の主張が正しいとき,その命題は真 (true)であるといい,正しくないとき偽 (false)であるという.
例えば,「寒い」という文は,人によって答えが変わってくるので命題ではない.しかし,「寒い」という言葉を「気温が10度以下」という条件で定義すると,「寒い」という文は命題となる.数学では明確に言葉を定義することが非常に重要である.
定義
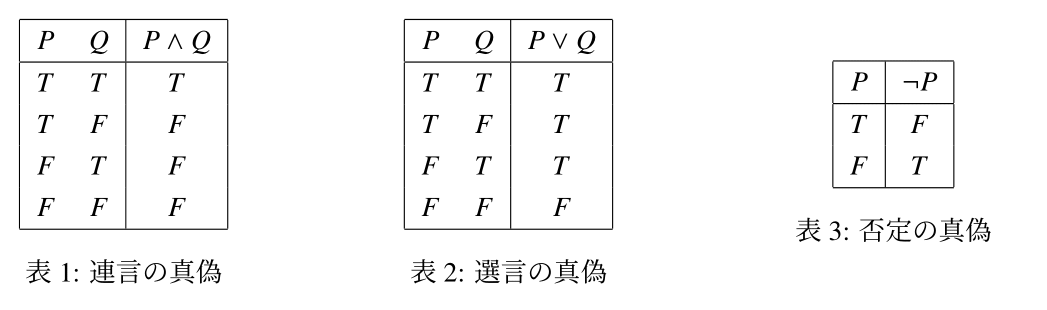
2つの命題$P$, $Q$について,「$P$かつ$Q$である」という命題を$P$と$Q$の連言 (conjunction)といい,$P \land Q$と表す.
$P \land Q$は,$P$と$Q$がともに真のときに真となり,$P$と$Q$のいずれかが偽のときには偽となる.
$P$と$Q$の真偽の組み合わせに応じた,連言の真偽を一覧にすると表1のようになる.この表のように命題どうしの真理値の対応を表した表を真理値表という.
定義
2つの命題$P$, $Q$について,「$P$であるか,または,$Q$である」という命題を$P$と$Q$の選言 (disjunction)といい,$P \lor Q$と表す.
$P \lor Q$は,$P$と$Q$のいずれかが真のときに真となり,$P$と$Q$がともに偽のときには偽となる.
$P$と$Q$がともに真のときにも真となることに注意すること.
$P$と$Q$の真偽の組み合わせに応じた,選言の真偽を一覧にすると表2のようになる.
定義
命題$P$について,「$P$ではない」という命題を$P$の否定 (negation)といい,$\lnot P$と表す.
$P$の真偽に応じた,否定の真偽を一覧にすると表3のようになる.