4回目:命題論理
4.1 論理同値,恒真命題と矛盾命題
定義
命題$P$と命題$Q$の真偽が常に一致することを論理同値 (equivalence)と言い,$P \iff Q$と書く.
つねに真となる命題のことを恒真命題 (tautology)とよび,$\top$と書く.
例えば,命題$P \lor \lnot P$ ($P$または$P$でない)は恒真命題である.
定義
常に偽となる命題のことを矛盾命題 (contradiction)とよび,$\bot$と書く.
例えば,命題$P \land \lnot P$ ($P$かつ$P$でない)は矛盾命題である.
4.2 計算法則
命題$P$, $Q$, $R$について,それぞれの命題の真偽によらず,つぎの関係が成り立つ.- 冪等律:$P \land P \Leftrightarrow P$
- 冪等律:$P \lor P \Leftrightarrow P$
- 交換律:$P \land Q \Leftrightarrow Q \land P$
- 交換律:$P \lor Q \Leftrightarrow Q \lor P$
- 結合律:$(P \land Q) \land R \Leftrightarrow P \land (Q \land R)$
- 結合律:$(P \lor Q) \lor R \Leftrightarrow P \lor (Q \lor R)$
- 分配律:$P \land (Q \lor R) \Leftrightarrow (P \land Q) \lor (P \land R)$
- 分配律:$P \lor (Q \land R) \Leftrightarrow (P \lor Q) \land (P \lor R)$
- 吸収律:$P \land (P \lor Q) \Leftrightarrow P$
- 吸収律:$P \lor (P \land Q) \Leftrightarrow P$
- 同一律:$P \lor \bot \Leftrightarrow P$
- 同一律:$P \land \top \Leftrightarrow P$
- 同一律:$P \lor \top \Leftrightarrow \top$
- 同一律:$P \land \bot \Leftrightarrow \bot$
- 補元律:$P \lor \lnot P \Leftrightarrow \top$
- 補元律:$P \land \lnot P \Leftrightarrow \bot$
- 補元律:$\lnot \top \Leftrightarrow \bot$
- 補元律:$\lnot \bot \Leftrightarrow \top$
- 対合律(二重否定):$\lnot \lnot P \Leftrightarrow P$
- ド・モルガンの法則:$\lnot P \land \lnot Q \Leftrightarrow \lnot (P \lor Q)$
- ド・モルガンの法則:$\lnot P \lor \lnot Q \Leftrightarrow \lnot (P \land Q)$
4.3 含意
定義
命題$P$と命題$Q$について,「$P$ならば$Q$」という命題を含意 (implication)と呼び,$P \rightarrow Q$と表す.
$P$と$Q$の真偽の組み合わせに応じた,含意の真偽を一覧にすると表1のようになる.
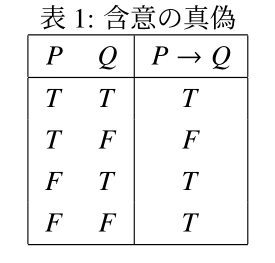
つまり,$P \to Q$は,$P$が真の命題で$Q$が偽の命題のとき,かつそのときに限り偽となる命題である.
$P$が偽の命題のときは$Q$の真偽に関わらず$P \to Q$は常に真となることに注意する.例えば,
「テストが60点未満」ならば「成績は不可である」という命題を考えよう.この場合,テストが60点未満の場合のみ成績が不可になることしか言っていない.仮にテストで70点取ったのにも関わらず成績が不可となったとしても,この命題に矛盾していない.$P \to Q$が1つの命題であることを意識しよう.

命題$P$, $Q$について,以下が成り立つ. \begin{eqnarray} P \rightarrow Q & \Leftrightarrow & \lnot P \lor Q \nonumber \\ P \rightarrow Q & \Leftrightarrow & \lnot Q \rightarrow \lnot P \nonumber \end{eqnarray}
定義
命題$P \rightarrow Q$に対して,$\lnot Q \rightarrow \lnot P$を$P \rightarrow Q$の対偶 (contraposition)という.
命題$P \rightarrow Q$とその対偶$\lnot Q \rightarrow \lnot P$は真偽が常に一致する.
定義
命題$P \rightarrow Q$に対して,$Q \rightarrow P$を$P \rightarrow Q$の逆 (converse)といい,
$\lnot P \rightarrow \lnot Q$を$P \rightarrow Q$の裏 (reverse)という.
一般に命題$P \rightarrow Q$とその裏の真偽が一致するとは限らないが,逆と裏は互いに対偶の関係にあるため,真偽は一致する.