1回目：カタラン数
凸多角形を対角線によって三角形に分割する操作を考える．一般に$n$角形を対角線によって三角形に分割するには，対角線を$n-3$本使う．例えば，四角形ならば，対角線は$2$本あるから，そのどちらかを使うかで，三角形への分割は$2$通りある．五角形ならば，下図のようにひとつの頂点から$2$本対角線を使うことで三角形に分割でき，以下のように$5$通りの三角形への分割がある．
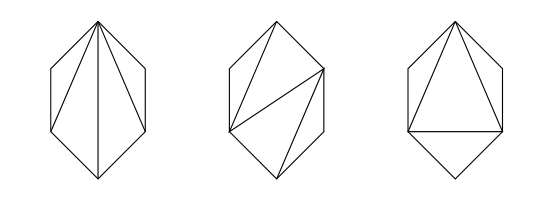
それでは一般の凸多角形に対して，対角線を引いて三角形に分割する方法は何通りあるであろうか． $n+2$角形に$n-1$本の対角線を引いて三角形に分割する方法の総数を$C_n$と書く． 便宜上$C_0=1$とする． この自然数$C_n$をカタラン数と呼ぶ． 上の説明から \[ C_1=1, C_2=2, C_3=5,C_4=14 \] である． この$C_n$対して，次のような漸化式が成り立つ．
命題 1.1
数列$\{C_n\}^{\infty}_{n=0}$は漸化式
\[
C_{n+1}=\sum_{i=0}^n C_i C_{n-i}
\]
を満たす．
証明
$(n+3)$角形の頂点を時計回りに$1,2,\ldots,n,n+1,n+2,n+3$とし，$1$と$2$を結ぶ辺を$e$とする．
$(n+3)$角形を三角形に分割したとき，$e$を含む三角形のもう一つの頂点を$i+3$とする．すると，この三角形により$(n+3)$角形は$(i+2)$角形と$(n-i+2)$角形に分割できる．
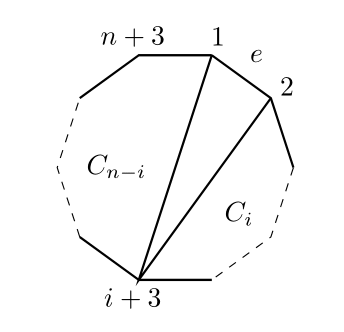それぞれの三角形への分割の総数はそれぞれ$C_i$と$C_{n-i}$であるので，$1,2,i+3$を頂点とする三角形を含む，$(n+3)$角形の三角形への分割の総数は$C_i C_{n-i}$である．
これを$0 \leq i\leq n$で考えると，それぞれ異なる三角形の分割が現れる．よって$(n+3)$角形の三角形への分割の総数は
\[
C_{n+1}=\sum_{i=0}^n C_i C_{n-i}
\]
である．
次にカタラン数の一般項を求めていく．
カタラン数を係数に持つ``形式的''冪級数$C(x)$を考える（詳しくは第12回で説明）：
\[
C(x):=\sum_{n=0}^{\infty} C_n x^n=C_0 + C_1 x + C_2 x^2 + \cdots.
\]
このとき次の命題が成り立つ．
命題 1.2
以下の等式が成り立つ：
\[
C(x)=\dfrac{1-\sqrt{1-4x}}{2x}.
\]
特に，
\[
C_n=\dfrac{1}{n+1}\binom{2n}{n}=\dfrac{(2n)!}{n!(n+1)!}
\]
である．
この命題の証明のために，二項係数と二項展開について説明する．
自然数$n$と非負整数$r \leq n$に対し，
\[
\binom{n}{r}=\dfrac{n(n-1)\cdots(n-r+1)}{r!}=\frac{n!}{(n-r)!r!}
\]
と定義する．つまり，$\binom{n}{r}$は高校数学で登場する二項係数$_n C_r$のことである．
$_n C_r$は$n$個から$r$個選ぶ方法の総数であったことを思い出そう．この二項係数を使い，自然数$n$に対し，
\[
(1+x)^n=\sum_{r=0}^n \binom{n}{r}x^r
\]
と表せるのを二項展開と呼んでいた．これを一般化する．
複素数$a$と非負整数$r$に対し
\[
\binom{a}{r}=\dfrac{a(a-1)\cdots(a-r+1)}{r!}
\]
と定義する．ただし，$\binom{a}{0}=1$とする．この一般化された二項係数を使うと，複素数$a$に対し，
\[
(1+x)^a=\sum_{r=0}^{\infty} \binom{a}{r}x^r
\]
が成り立つ．これは単に，$(1+x)^a$の$x=0$におけるテイラー展開であるが，``形式的''冪級数を考える上では，$x$に値を代入するといった解析的意味はないので，いつでもこのように表記できる．
それでは命題1.2を証明する．
命題1.2の証明
$C(x)^2$の$x^n$の係数を考えると，これは
$ \sum_{i=0}^nC_i C_{n-i}
$ である（実際，次数の低いところから考えてみよう）．
つまり，
\[
C(x)^2=\sum_{n=0}^{\infty} \left( \sum_{i=0}^n C_i C_{n-i} \right) x^n
\]
となる．すると命題1.1から
\[
C(x)^2=\sum_{n=0}^{\infty} C_{n+1} x^n
\]
となる．そこで$xC(x)^2$を考えると，
\begin{align*}
xC(x)^2&=x\sum_{n=0}^{\infty} C_{n+1} x^n
=\sum_{n=0}^{\infty} C_{n+1} x^{n+1}\\
&=\sum_{n=1}^{\infty} C_n x^n
=C(x)-1
\end{align*}
と変形できる．この等式を$C(x)$に関する$2$次方程式と思い解くと，
\[
C(x)=\dfrac{1\pm \sqrt{1-4x}}{2x}
\]
となる．
$C(x)=\dfrac{1+ \sqrt{1-4x}}{2x}$のとき，二項展開から
\[
C(x)=\dfrac{1+(1-2x-2x^2-\cdots)}{2x}=\dfrac{1}{x}-1-x-\cdots
\]
となり不適切である．
よって
$C(x)=\dfrac{1- \sqrt{1-4x}}{2x}$である．
すると
\begin{align*}
C(x)&=\dfrac{1- \sqrt{1-4x}}{2x}\\
&=\dfrac{1-\displaystyle\sum_{n=0}^{\infty}\binom{\frac{1}{2}}{n}(-4x)^n}{2x}\\
&=\sum_{n=0}^{\infty}\dfrac{1}{n+1}\binom{2n}{n}x^n
\end{align*}
となるので
\[
C_n=\dfrac{1}{n+1}\binom{2n}{n}=\dfrac{(2n)!}{n!(n+1)!}
\]
である．
さて，カタラン数の定義を思い出すと，自然数$n$に対して，$\mathcal{T}_n$で$(n+2)$角形を三角形に分割する方法全体の集合としたとき，$C_n=|\mathcal{T}_n|$で定義される．実は，これ以外の数え上げを使ってカタラン数を定義する方法はたくさんある．つまり，$n$に関する何かしらの集合$\mathcal{S}_n$で$C_n=|\mathcal{S}_n|$を満たすものが存在する．
ある集合$\mathcal{S}_n$が$C_n=|\mathcal{S}_n|$を満たすことの証明方法として，一つは$|\mathcal{S}_n|$が命題1.1の漸化式を満たすことを証明すればよい．もう一つの方法として$\mathcal{S}_n$と$\mathcal{T}_n$の間の全単射写像が存在することを証明，つまりこのような写像を具体的に構成するという方法がある．
後者の証明方法を組合せ論的証明という．
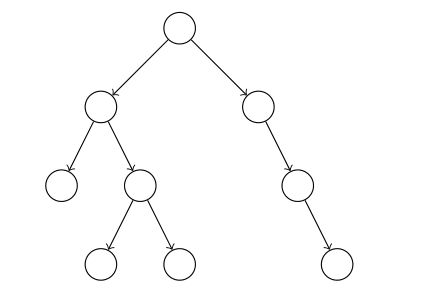
例えば，二分木と呼ばれるデータ構造がある．これは1つの頂点（親）から出発し，高々２つの頂点（子）に分かれていく図のことである（分かれ方は左右で区別する）． 下図は9頂点の二分木である．
命題 1.3
$\mathcal{T}_n$と$\mathcal{B}_n$の間には全単射写像が存在する．特に，
\[
C_n=|\mathcal{B}_n|
\]
である．
詳細は述べないが，
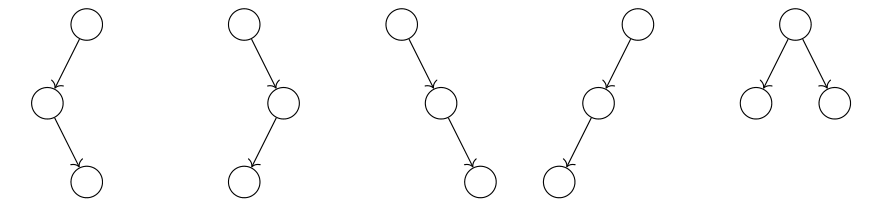
例えば$n=3$の場合，以下のような対応を考えて全単射を構成している．
