2回目：オイラーの多面体定理
定理 2.1 (オイラーの多面体定理)
凸多面体$\mathcal{P}$の頂点の個数，辺の個数，面の個数をそれぞれ$v,e,f$とする．
このとき，
\[
v-e+f=2
\]
が成り立つ．
この定理は高校の数学Aの教科書に書かれているが特に証明は書かれていない．ここではこの定理の証明を与える．そもそも「凸多面体」の厳密な定義は何であろうか．高校の教科書を見ると「平面で囲まれた立体を多面体といい，凹みのない多面体を凸多面体という」と書いてある．これは「数学的な定義」ではなく，直感的な定義である．実は厳密に凸多面体を定義しようとすると色々準備が必要である．さらに頂点，辺，面を定義するのにもさらなる準備が必要となってくる．しかし，この講義でこれらを１から定義するのは本質から外れるので，一旦飛ばしてオイラーの多面体定理の証明を行う．
まず，2次元，つまり凸多角形のことを考える．
定義 2.2
平面の有限個の凸多角形の集合$\Gamma=\{\mathcal{P}_1,\mathcal{P}_2,\ldots,\mathcal{P}_n\}$に対し，
次の条件が満たされるとき，$\Gamma$を凸多角形の貼り合せと呼ぶ：
これは多角形をいくつかの凸多角形を「綺麗に」貼り合わすことで構成する操作である．
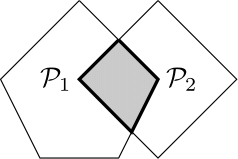
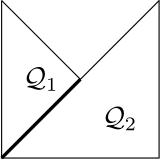
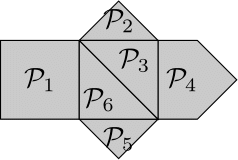
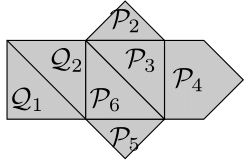
例えば，下図の集合$\{\mathcal{P}_1,\mathcal{P}_2\}$や$\{\mathcal{Q}_1,\mathcal{Q}_2\}$は条件(1)を満たしていない．
- $i \neq j$のとき，$\mathcal{P}_i \cap \mathcal{P}_j \neq \emptyset$であれば，$\mathcal{P}_i \cap \mathcal{P}_j$は$\mathcal{P}_i$の辺または頂点であり，かつ$\mathcal{P}_j$の辺または頂点である．
- 平面図形$\mathcal{P}_1 \cup \cdots \cup \mathcal{P}_n$は（凸とは限らない）多角形である．この多角形を$|\Gamma|$と表し，$\Gamma$に付随する多角形と呼ぶ．
命題 2.3
凸多角形の貼り合せ$\Gamma$の頂点の個数，辺の個数，面の個数をそれぞれ$v,e,f$とする．
このとき，
\[
v-e+f=1
\]
が成り立つ．
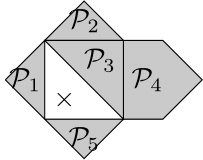
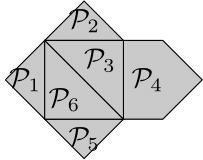
上記の凸多面体の貼り合わせの例である$\{\mathcal{P}_1,\mathcal{P}_2,\mathcal{P}_3,\mathcal{P}_4,\mathcal{P}_5,\mathcal{P}_6\}$だと$v=10,e=15,f=6$で確かに
\[
v-e+f=10-15+6=1
\]
が成り立つ．それでは証明していく．
証明
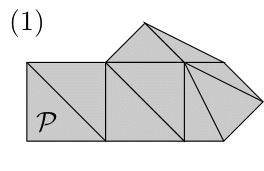
（第一段）$\Gamma=\{\mathcal{P}_1,\ldots,\mathcal{P}_n\}$とする．もし$\mathcal{P}_1$が三角形でないとすると，$\mathcal{P}_1$に対角線を1本引いて$\mathcal{P}_1$を$\mathcal{Q}_1$と$\mathcal{Q}_2$に分割し，凸多角形の貼り合せ$\Gamma'=\{\mathcal{Q}_1,\mathcal{Q}_2,\mathcal{P}_2,\ldots,\mathcal{P}_n\}$を考える．
すると$\Gamma'$は$\Gamma$よりも辺が$1$本増え，面も$1$個増える．ただし，頂点の個数は変わらない．よって$\Gamma'$と$\Gamma$で$v-e+f$の値は変わらない．したがって，$\Gamma'$で$v-e+f=1$を証明すればよい．
（第二段）凸$n$多角形は，１つの頂点を選び，その頂点から隣り合わない頂点に対角線を引けば，三角形に分割できる．すると第一段の操作を繰り返せば，結局$\Gamma$のすべての面が三角形のときに，$v-e+f=1$を示せばよい（このような三角形のみからなる貼り合せを三角形の貼り合せ}または三角形分割}と呼ぶ）．
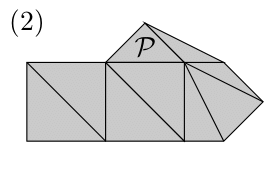
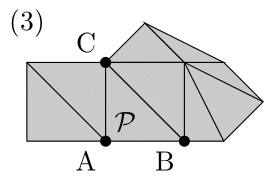
（第三弾）$n$に関する帰納法で証明する．$n=1$のとき，つまり$\Gamma$がただ1つの三角形からなるときは，明らかに主張が成り立つ．$n \geq 2$とし，$\Gamma=\{\mathcal{P}_1,\ldots,\mathcal{P}_n\}$を三角形の貼り合せとする．$\Gamma$の面の中で，少なくとも1つの辺が$|\Gamma|$の境界に含まれるものを任意に選ぶ．その面を$\mathcal{P}$とし，さらにその頂点を$A,B,C$とする．このとき，次の3つの可能性がある．
（1）と（2）の場合，$\Gamma$から$\mathcal{P}$を除いた$\Gamma \setminus \{\mathcal{P}\}$も三角形の貼り合せであって，$v-e+f$は不変である．すると帰納法の仮定から主張が成り立つ．
（3）の場合，$\Gamma$から$\mathcal{P}$を除いた$\Gamma \setminus \{\mathcal{P}\}$は三角形の貼り合せにならないことに注意する．実際，$|\Gamma|$の境界に含まれる$\mathcal{P}$の辺を$AB$としたとき，$\Gamma \setminus \{\mathcal{P}\}$は2つの多角形の貼り合せが頂点$C$で繋がったものになる．
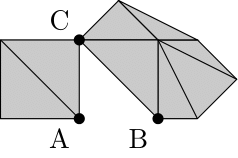その2つ多角形の貼り合せを$\Gamma_1$と$\Gamma_2$とする．ここで$\Gamma_1$と$\Gamma_2$は三角形の貼り合せである．$\Gamma_1$と$\Gamma_2$の頂点の個数，辺の個数，面の個数をそれぞれ$v_1,v_2,e_1,e_2,f_1,f_2$とする．すると，
\[
f=f_1+f_2+1, e=e_1+e_2+1, v=v_1+v_2-1
\]
が成り立つ．帰納法の仮定を$\Gamma_1$と$\Gamma_2$に用いると
\[
v_1-e_1+f_1=v_2-e_2+f_2=1
\]
を得るので，以上から
\[
v-e+f=(v_1+v_2-1)-(e_1+e_2+1)+(f_1+f_2+1)=(v_1-e_1+f_1)+(v_2-e_2+f_2)-1=1
\]
となり，主張が成り立つ．
それではオイラーの多面体定理を証明する．
（第二段）凸$n$多角形は，１つの頂点を選び，その頂点から隣り合わない頂点に対角線を引けば，三角形に分割できる．すると第一段の操作を繰り返せば，結局$\Gamma$のすべての面が三角形のときに，$v-e+f=1$を示せばよい（このような三角形のみからなる貼り合せを三角形の貼り合せ}または三角形分割}と呼ぶ）．
（第三弾）$n$に関する帰納法で証明する．$n=1$のとき，つまり$\Gamma$がただ1つの三角形からなるときは，明らかに主張が成り立つ．$n \geq 2$とし，$\Gamma=\{\mathcal{P}_1,\ldots,\mathcal{P}_n\}$を三角形の貼り合せとする．$\Gamma$の面の中で，少なくとも1つの辺が$|\Gamma|$の境界に含まれるものを任意に選ぶ．その面を$\mathcal{P}$とし，さらにその頂点を$A,B,C$とする．このとき，次の3つの可能性がある．
- $\mathcal{P}$の2つの辺が$|\Gamma|$の境界に含まれる．
- $\mathcal{P}$の1つの辺が$|\Gamma|$の境界に含まれるが，その辺に属さないもう1つの頂点は$|\Gamma|$の境界に含まれない．
- $\mathcal{P}$の1つの辺が$|\Gamma|$の境界に含まれており，その辺に属さないもう1つの頂点も$|\Gamma|$の境界に含まれる．
定理 2.1の証明
凸多面体$\mathcal{P}$の任意の面$\mathcal{F}$を1つ選び，$\mathcal{P}$から面$\mathcal{F}$を除去し，$\mathcal{P}$に穴を開ける．ただし，$\mathcal{F}$の辺と頂点はそのまま残す．次に，穴が上になるように凸多面体$\mathcal{P}$を置き，さらに$\mathcal{P}$の内部は空洞で，境界が弾性のゴムでできていると仮定する．今，その穴を十分大きく広げて，平面に押しつぶすと，その平面に$\mathcal{P}$の$\mathcal{F}$以外の面からなる凸多角形の貼り合せができる．
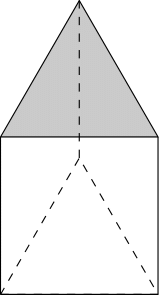
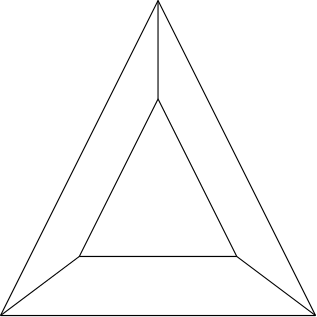この貼り合せの面の個数は$f-1$，辺の個数は$e$，頂点の個数は$v$であるので，命題2.3を使うと
\[
v-e+(f-1)=1
\]
より，
\[
v-e+f=2
\]
が得られる．