4回目：平面グラフと5色定理
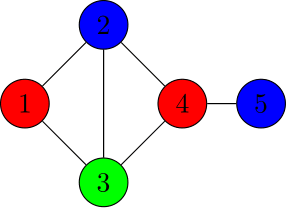
オイラーの多面体定理（の類似）の応用をもう一つ紹介する． 平面グラフとは，平面上のいくつかの頂点とそれらを交差なく結ぶいくつかの辺から構成された図形である．例えば，以下の図は頂点集合を$\{1,2,3,4\}$とし，辺集合を$\{ \{1,2\}, \{2,3\},\{1,4\}\}$とする平面グラフを表す．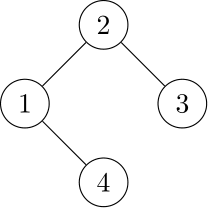
定理 4.1 (オイラーの定理)
平面グラフ$G$に対し，その頂点数，辺数，面数をそれぞれ$|V|,|E|,|F|$とする．
このとき，
\[
|V|-|E|+|F|=2
\]
が成り立つ．
この定理を使って5色定理というものを証明する．
今，（任意の）世界地図に対して，隣接する国同士が異なる色になるように，国に色を塗っていく．
例えば次のような色の塗り方である．
- $G$の頂点は地図の国に対応．
- 2つの国が地図で隣接しているとき，その国に対応する頂点同士を辺で結ぶ．
定理 4.2 (4色定理)
$G$を平面グラフとする．このとき，$\chi(G) \leq 4$である．
つまり，上記のルールで国に色を塗るためには$4$色あれば十分ということである．
この定理は1879年にKempeが証明したと発表したが，1890年に証明の不備が発見された．そしてしばらくの間はこの定理は未解決であったが，1976年にAppelとHakenが計算機を使って膨大な場合わけの検証の結果，証明を完成させた．しかし，数学において計算機を用いた証明は完全には認められないため，本当の意味でこの定理を証明したことには至っていない．ただし，計算機の発展により，ほとんどの人は4色定理はほぼ解決したと認めている．4色定理の理論的証明ができれば，世界で最も有名な数学者の1人になれるであろう．
さて，Kempeの証明は残念ながら4色定理の証明には至らなかったが，同じ手法で5色定理を証明することができる．
定理 4.3 (5色定理)
$G$を平面グラフとする．このとき，$\chi(G) \leq 5$である．
この定理の証明のために1つ補題を準備する．
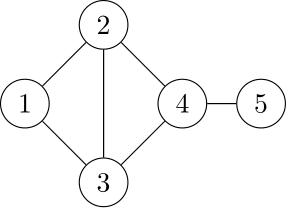
グラフ$G$の頂点$v$に対し，$v$に辺で結ばれている頂点の個数を$v$の次数という．
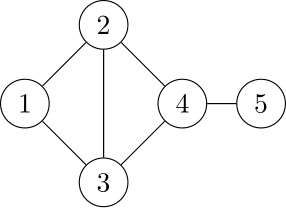
下図の場合，頂点$1$と$4$の次数は$2$，頂点$2$と$3$の次数は$3$，頂点$5$の次数は$1$である．
補題 4.4
平面グラフ$G$は次数が$5$以下の頂点が少なくとも$1$つ持つ．
証明
平面グラフ$G$の全ての頂点の次数が$6$以上と仮定する．$G$の頂点数，辺数，面数をそれぞれ$|V|,|E|,|F|$とする．
各頂点に$6$本以上の辺が結ばれているので
\[
6|V| \leq 2|E|
\]
が成り立つ．
一方，各面には少なくとも$3$本以上の辺が含まれているので，
\[
3|F| \leq 2|E|
\]
が成り立つ．
これをオイラーの定理に代入すると
\[
2=|V|-|E|+|F| \leq \frac{1}{3}|E|-|E|+\frac{2}{3}|E|=0
\]
となり矛盾する．よって平面グラフ$G$は次数が$5$以下の頂点が少なくとも$1$つ持つ．
それでは$5$色定理を証明する．
5色定理の証明
頂点の個数$|V|$に関する帰納法で証明する．$|V|=1$のときは$1$色で十分であるので成り立つ．
$|V| \leq 2$とする．グラフ$G$には補題4.4から次数が$5$以下の頂点が存在する．そのうちの一つを$v$とする．$G$から$v$と$v$に接続する辺を全て取り除いたグラフ$G-v$を考えると，$G-v$は平面グラフでありその頂点数は$|V|-1$である．よって帰納法の仮定から$G-v$は頂点を5色で塗ることができる．その塗り方を一つ固定する．$v$の次数が$G$の中で$4$以下であれば，$v$に接続する頂点に塗られていない色を$G$の中で塗ることができ，その場合は定理が成り立つことになる．
今，$v$の次数は$5$であると仮定する．$v$に接続する頂点が$4$色以下で塗られているときは，上記と同様で$G$は5色で塗ることができる．よって$v$に接続する5頂点は$5$色で塗られていると仮定する．このとき，$v$を中心に$v$に接続する5つの頂点は以下のように時計回りに配置されているとする．
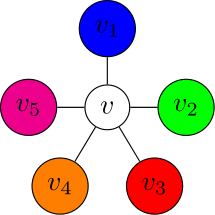それぞれの頂点を$v_1,v_2,\ldots,v_5$，さらにそれぞれの頂点に塗られている色を$1,2,\ldots,5$とする．頂点$v_1$に注目し，$v_1$から色$1$（青）と$3$（赤）で塗られている頂点を辿ってできる道を考える．もしどの道も$v_3$に接続しないのであれば，その道の頂点の色$1$と$3$をすべて入れ替えることができる．実際，この道上にない頂点は他の色が塗られているか，この道に接続しないからである．すると頂点$v$に色$1$（青）を塗ることができ，この場合は定理が成り立つ．
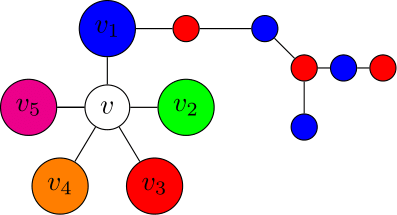
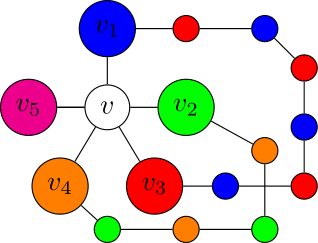
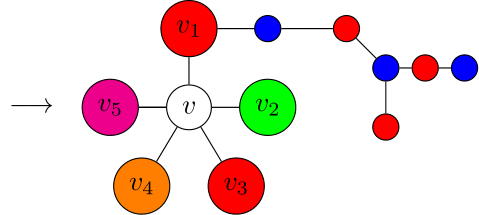そこで$v_1$から色$1$と$3$で塗られている頂点を辿ってできる道で，$v_3$に接続するものがあると仮定する．それを$P$とする．次に$v_2$に注目し，今度は$v_2$から色$2$と$4$で塗られている頂点を辿ってできる道を考える．もしどの道も$v_4$に接続しないのであれば，上記と同じ議論で定理が成り立つ．
そこで$v_4$に接続する道があると仮定する．
しかしこの道は必ず$P$と交わってしまい，$G$が平面グラフであることに矛盾する．
以上より証明が完了した．
今，$v$の次数は$5$であると仮定する．$v$に接続する頂点が$4$色以下で塗られているときは，上記と同様で$G$は5色で塗ることができる．よって$v$に接続する5頂点は$5$色で塗られていると仮定する．このとき，$v$を中心に$v$に接続する5つの頂点は以下のように時計回りに配置されているとする．