5回目：一般次元の凸多面体

ここまでは凸多角形や凸多面体に関するオイラーの多面体定理を紹介してきたが，凸多面体は4次元以上でも定義でき，さらにオイラーの多面体定理も成り立つ．まずは一般次元の凸多面体を定義していく．$\mathbb{R}^d$で$d$次元の実空間を表す．

定義 5.1

$\mathbb{R}^d$上の集合$A$が凸集合であるとは，$A$に含まれる任意の2点$\mathbf{a},\mathbf{b} \in \mathbb{R}^d$について$\mathbf{a}$と$\mathbf{b}$を結ぶ線分 \[ [\mathbf{a}, \mathbf{b}]:=\{ \lambda \mathbf{a} + (1-\lambda) \mathbf{b} : 0 \leq \lambda \leq 1\} \subset \mathbb{R}^d \] が再び$A$に含まれるときにいう．

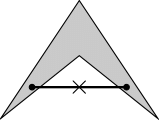
例えば，三角形や四角形，立方体や三角柱，円や球などは凸集合である．一方，下図のような「凹み」がある図形は凸ではない．実際，凹んでいる近くの2点を結ぶとその線分は図形に含まれない．

凸集合の共通部分は凸集合である．実際，以下が成り立つ．

補題 5.2

$\mathbb{R}^d$の空でない凸集合の族$\{\mathcal{A}_i\}_{i \in I}$を考える．ここで$I$は添字集合である．このとき， \[ \mathcal{A} = \bigcap_{i \in I} \mathcal{A}_i \] は凸集合である．

証明

$\mathcal{A}$に含まれる任意の$2$点$\mathbf{x},\mathbf{y}$をとる．任意の$i \in I$について，$\mathcal{A} \subset \mathcal{A}_i$であるから，$\mathbf{x},\mathbf{y} \in \mathcal{A}_i$が成り立ち，さらに$\mathcal{A}_i$は凸集合であるから線分$[\mathbf{x},\mathbf{y}]$は$\mathcal{A}_i$に含まれる．特に線分$[\mathbf{x},\mathbf{y}]$は$\mathcal{A}$に含まれる．よって$\mathcal{A}$は凸集合である．

例えば，複数の円を書いたとき，重なっている部分は凸集合となっている．この補題より次の系が従う．

系 5.3

$\mathbb{R}^d$の空でない部分集合$V$に対し，$V$を含む最小の凸集合が存在する．つまり凸集合$V \subset \mathcal{A}$で，任意の凸集合$V \subset \mathcal{B}$に対し，$\mathcal{A} \subset \mathcal{B}$となるものが存在する．

証明

部分集合$V$を含む凸集合全てからなる集合族を$\{\mathcal{A}_i\}_{i \in I}$とし， \[ \mathcal{A} = \bigcap_{i \in I} \mathcal{A}_i \] とする． $\mathbb{R}^d$は$V$を含む（最大の）凸集合であるのでこの集合族は空ではない．すると補題5.2より，$\mathcal{A}$は凸集合である．もし，$V \subset \mathcal{B} \subsetneq \mathcal{A}$を満たす凸集合$\mathcal{B}$があったとしたら，$\mathcal{B} \in \{\mathcal{A}_i\}_{i \in I}$であり， \[\mathcal{A} = \bigcap_{i \in I} \mathcal{A}_i \subset \mathcal{B} \subsetneq \mathcal{A} \]となるので矛盾．よって$\mathcal{A}$は$V$を含む最小の凸集合である．

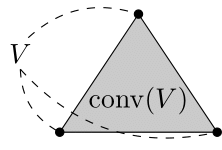
$V$を含む最小の凸集合を${\rm conv}(V)$で表し，$V$の凸閉包という．下図のように凸閉包は$V$の内側を塗りつぶすイメージである．

この凸閉包を用いて凸多角形と凸多面体が定義できる．

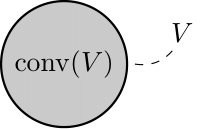
定義 5.4

空間$\mathbb{R}^d$の部分集合$\mathcal{P}$が凸多面体であるとは，有限集合$V \subset \mathbb{R}^d$で$\mathcal{P}={\rm conv}(V)$となるものが存在するときにいう．

凸多面体の定義で重要なのは$V$が有限集合ということである．実際，円を凸閉包を使って表そうとすると，少なくとも円周の全ての点（これは無限個）が必要である．有限個の点の凸閉包が角張った図形を表しているのである．次に凸多面体の次元を定義するために，少し用語を準備する．

定義 5.5

空間$\mathbb{R}^d$の点の集合$\{\mathbf{a}_0,\mathbf{a}_1,\ldots,\mathbf{a}_n\}$がアフィン独立であるとは，$\{\mathbf{a}_1-\mathbf{a}_0,\mathbf{a}_2-\mathbf{a}_0,\ldots,\mathbf{a}_n-\mathbf{a}_0\}$が1次独立であるときにいう．つまり， \[ \lambda_1(\mathbf{a}_1-\mathbf{a}_0)+\lambda_2(\mathbf{a}_2-\mathbf{a}_0)+ \cdots + \lambda_n(\mathbf{a}_n-\mathbf{a}_0)=\mathbf{0} \Longrightarrow \lambda_1=\cdots=\lambda_n=0\] が成り立つときにいう．

定義 5.6

凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し，$\mathcal{P}$に含まれるアフィン独立な集合のうち，その集合に属する点の最大個数を$n+1$とする．このとき，$\mathcal{P}$の次元を$n$と定義し，$\dim(\mathcal{P})$と書く．つまり， \[ \dim (\mathcal{P})=\max( |V|-1 : V\mbox{は$\mathcal{P}$のアフィン独立な部分集合}) \]また$2$次元凸多面体のことを凸多角形という．

例えば，$V=\{(0,0),(1,0),(0,1)\}$としたときの凸多面体$\mathcal{P}={\rm conv}(V)$を考えると，$\mathcal{P}$は$2$次元凸多面体，つまり凸多角形である．一方，$V=\{(1,0,0),(0,1,0),(0,0,1)\}$としたときの凸多面体$\mathcal{P}={\rm conv}(V)$も凸多角形である．また$\mathcal{P}=\{ (x_1,\ldots,x_d) \in \mathbb{R}^d : 0 \leq x_i \leq 1, \forall i\}$は$d$次元凸多面体である（この凸多面体を$d$次元超立方体と呼ぶ）．

次に一般次元の面の定義を行う．空間$\mathbb{R}^d$の超平面 (hyperplane)とは$(a_1,\ldots,a_d) \in \mathbb{R}^d$と実数$b$を使い， \[ \mathcal{H}=\{ (x_1,\ldots,x_d) \in \mathbb{R}^d : a_1 x_1 + \cdots +a_d x_d =b \} \] と表示される集合$\mathcal{H} \subset \mathbb{R}^d$のことである．ただし，$(a_1,\ldots,a_d) \neq (0,\ldots,0)$である．%超平面は次元$d-1$の$\mathbb{R}^d$のアフィン空間である．また空間$\mathbb{R}^d$の部分集合 \begin{align*} \mathcal{H}^{(+)} &= \{ (x_1,\ldots,x_d) \in \mathbb{R}^d : a_1 x_1 + \cdots +a_d x_d \geq b \},\\ \mathcal{H}^{(-)} &= \{ (x_1,\ldots,x_d) \in \mathbb{R}^d : a_1 x_1 + \cdots +a_d x_d \leq b \} \end{align*} を超平面$\mathcal{H}$が定義する閉半空間という．凸多面体$\mathcal{P} \subset \mathbb{R}^d$の支持超平面とは，次の条件を満たす空間$\mathbb{R}^d$の超平面$\mathcal{H}$のことである：

$\mathcal{P} \subset \mathcal{H}^{(+)}$または$\mathcal{P} \subset \mathcal{H}^{(-)}$である．
$\mathcal{P} \cap \mathcal{H} \neq \emptyset$かつ$\mathcal{P} \cap \mathcal{H} \neq \mathcal{P}$である．

例 5.7

下図のような三角形$\mathcal{P}$と直線$L_1,\ldots,L_6$を考えると$L_1,L_2,L_3,L_4$は支持超平面であるが，$L_5$と$L_6$は支持超平面ではない．

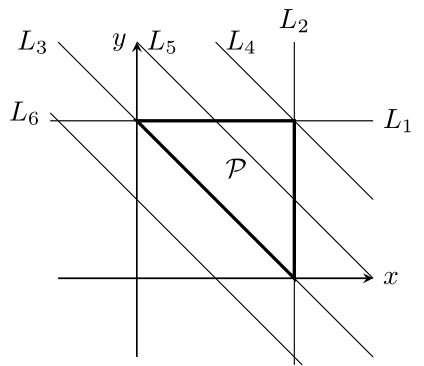
凸多面体$\mathcal{P}$とその支持超平面$\mathcal{H}$の共通部分$\mathcal{P} \cap \mathcal{H}$は再び凸多面体となる．例えば，上の例で$\mathcal{P} \cap L_1,\mathcal{P} \cap L_2,\mathcal{P} \cap L_3$は$\mathcal{P}$の辺， $\mathcal{P} \cap L_4$は頂点となっている．実はこのようにして得られる凸多面体が$\mathcal{P}$の面である．

定義 5.8

$\mathcal{P} \subset \mathbb{R}^d$を$d$次元凸多面体とし，$\mathcal{H}$を$\mathcal{P}$の支持超平面とする．このとき，$\mathcal{F}=\mathcal{P} \cap \mathcal{H}$を$\mathcal{P}$の面という．特に，$\dim \mathcal{F}=i$のとき，$i$面といい，$0$面のことを頂点，$1$面のことを辺， $(d-1)$面のことをファセットという．

こうすることで，これまで曖昧だった頂点や辺，面の定義が厳密にできた．実際，上図の例では$\mathcal{P} \cap L_4$は$\mathcal{P}$の頂点であり，$\mathcal{P} \cap L_1$は辺（かつファセット）である．また頂点には次のような性質がある．

命題 5.9

凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し，$V=\{\mathbf{v}_1,\ldots,\mathbf{v}_n\}$を$\mathcal{P}$の頂点全体の集合とする．このとき， \[ \mathcal{P} = {\rm conv}(V) \] であり，$V$はこの等式を満たす最小の集合である．

つまり頂点は凸多面体を構成する最小の情報である．すると頂点は「端っこの点」であり，これまで登場した頂点と同じであることが想像できるであろう．それではオイラーの多面体定理の高次元版を紹介する．$d$次元凸多面体$\mathcal{P}$と整数$0 \leq i \leq d-1$に対し，$\mathcal{P}$の$i$面の個数を$f_i$で表す．また数列$f(\mathcal{P})=(f_0,f_1,\ldots,f_{d-1})$を$\mathcal{P}$の$f$列と呼ぶ．

定理 5.10 (オイラーの多面体定理の一般次元版)

次元$d \geq 2$の凸多面体$\mathcal{P}$に対し，等式 \[f_0-f_1+f_2-\cdots+(-1)^{d-1} f_{d-1} = 1 + (-1)^{d-1}\] が成り立つ．

証明は難しくないがかなり複雑である．興味のある人は大学院の講義「離散数学特論（3回目）」を見てほしい．

$3$次元の場合と同様に，$h$列が定義できる． $\mathcal{P}$の$h$列$h(\mathcal{P})=(h_0,h_1,\ldots,h_d)$を次の公式で定義する： \[ \sum_{i=0}^d f_{i-1} (x-1)^{d-i}=\sum_{i=0}^d h_i x^{d-i}． \] ただし，$f_{-1}=1$である．頂点の個数が最小の$d$次元凸多面体，つまり$d+1$頂点の$d$次元凸多面体のことを単体と呼ぶ．例えば，三角形や四面体は単体である．すべての面が単体であるような凸多面体のことを単体的凸多面体と呼ぶ．このとき，$3$次元の場合と同様に，単体的凸多面体の$h$列は対称となる．

定理 5.11 (Dehn--Sommerville方程式)

$d$次元単体的凸多面体$\mathcal{P}$に対し， \[ h_i=h_{d-i}, \ \ \ \ 0 \leq i \leq d \] が成り立つ．

離散数学