6回目：ピックの公式
座標平面上の点が格子点であるとは，その点の$x$座標と$y$座標がともに整数となるときにいう． 平面上の（凸とは限らない）多角形が格子多角形であるとは，その多角形のすべての頂点が格子点であるときにいう．格子多角形$\mathcal{P}$に対し，その内部に含まれる格子点の個数を$i(\mathcal{P})$，境界に含まれる格子点の個数を$b(\mathcal{P})$，$\mathcal{P}$の面積を$A(\mathcal{P})$と書くことにする．定理 6.1 (ピックの公式)
平面上の格子多角形$\mathcal{P}$に対し，
\[
A(\mathcal{P})=i(\mathcal{P})+\frac{b(\mathcal{P})}{2}-1
\]
が成り立つ．
例えば以下の格子多角形の面積を求めてみる．
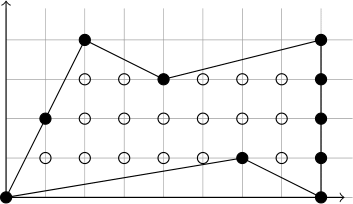
それではピックの公式の証明に向けて準備を行う． 平面上の格子三角形が頂点以外に格子点を含まないとき，つまり$i=0$かつ$b=3$のとき，空三角形}と呼ぶ．例えば，以下の三角形はすべて空三角形である．
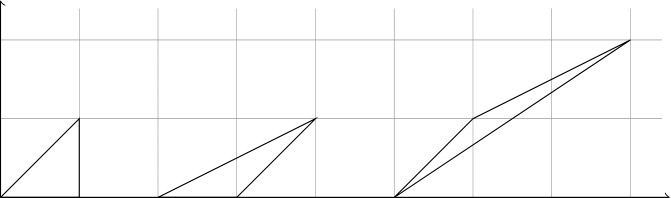
補題 6.2
空三角形の面積は$\frac{1}{2}$である．
証明
（第1段）座標軸に平行な辺を持つ格子長方形$\mathcal{Q}$についてピックの公式が成り立つことを示す．便宜上このような長方形を特殊格子長方形}という．
$\mathcal{Q}$は水平方向と垂直方向に移動し，別の格子長方形に移しても，その内部と境界に含まれる格子点の個数は不変である．よって$\mathcal{Q}$の頂点の座標を$(0,0),(s,0),(0,t),(s,t)$としてよい．ただし$s,t \geq 1$である．
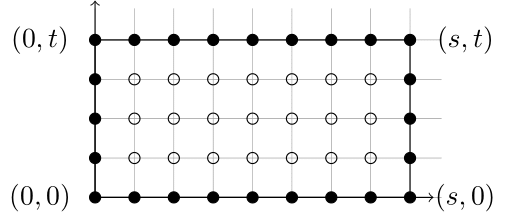この場合，内部に含まれる格子点の個数は$i(\mathcal{Q})=(s-1)(t-1)$であり，境界に含まれる格子点の個数は$b(\mathcal{Q})=2(s+t)$となる．すると，
\[
i(\mathcal{Q})+\frac{b(\mathcal{Q})}{2}-1=(s-1)(t-1)+(s+t)-1=st
\]
となり，これはこの長方形の面積と一致する．
（第2段） 斜辺以外の辺が座標軸に平行である直角三角形$\mathcal{P}$についてピックの公式が成り立つことを示す．便宜上このような三角形を特殊格子三角形}という． そのような直角三角形は（第1段）の長方形$\mathcal{Q}$を対角線$L$で切り取ることで得られる．
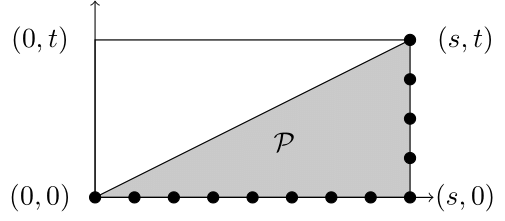（第1段）の記号を踏襲し，$L$は$(0,0)$と$(s,t)$を結ぶ線分とし，$\mathcal{P}$は下側の直角三角形とする．
対角線$L$に含まれる両端を除く格子点の個数を$q$とすると，$\mathcal{P}$の境界に含まれる格子点の個数は
$b(\mathcal{P})=q+s+t+1$である．次に長方形$\mathcal{Q}$の内部に含まれる格子点の個数$i(\mathcal{Q})$は$2i(\mathcal{P})+q$である．（第1段）の計算結果から
$i(\mathcal{Q})=(s-1)(t-1)$であるから
$i(\mathcal{P})=\frac{st-(s+t)+1-q}{2}$である．すると，
\[
i(\mathcal{P})+\frac{b(\mathcal{P})}{2}-1=\frac{st-(s+t)+1-q}{2}+\frac{q+s+t+1}{2}-1=\frac{st}{2}
\]
となり，$\mathcal{P}$の面積と一致する．
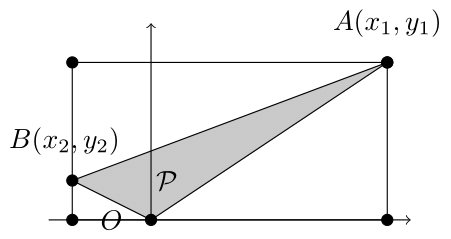
（第3段）いま，格子三角形$\mathcal{P}$があったとき，その頂点の座標をO$=(0,0)$, A$=(x_1,y_1)$, B$=(x_2,y_2)$とし，$0 < y_1, 0 \leq y_2 \leq y_1, 0 \leq x_1$としてよい（平行移動，$x$軸と$y$軸について対称に動かせばよい）． これを
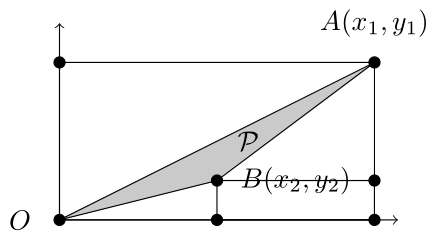
(ii)の場合は3個以下の特殊三角形と1個以下の特殊格子長方形を$\mathcal{P}$に貼り合わせれば，特殊格子長方形となる．
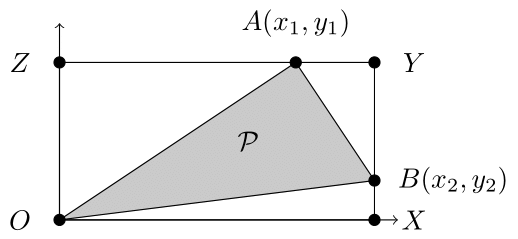
$\mathcal{P}$が空三角形であるとし，(i)の$x_1 \leq x_2$の場合に対して補題の主張を証明する．(i)の$x_2 \leq 0$と(ii)の場合は演習問題とする．
${\rm X}=(x_2,0)$, ${\rm Y}=(x_2,y_1)$, ${\rm Z}=(0,y_1)$とし，特殊格子三角形ABY，OBX，OAZをそれぞれ$\mathcal{P}_1,\mathcal{P}_2,\mathcal{P}_3$，特殊格子長方形OXYZを$\mathcal{Q}$とする．
すると$\mathcal{P}$は頂点以外に格子点を含まないので，
\[i(\mathcal{P}_1)+i(\mathcal{P}_2)+i(\mathcal{P}_3)=i(\mathcal{Q})=(x_2-1)(y_1-1)\]
となる．一方，辺OA, OB, ABは両端以外に格子点を含まないことに注意すると，
\[
b(\mathcal{P}_1)+b(\mathcal{P}_2)+b(\mathcal{P}_3)=b(\mathcal{Q})+3=2x_2+2y_1+3
\]
である．（第1段）と（第2段）の結果を用いると，三角形ABY, OBX, OAZの面積の和は
\begin{align*}
A(\mathcal{P}_1)+A(\mathcal{P}_2)+A(\mathcal{P}_3)&=
(i_1+i_2+i_3)+\frac{b_1+b_2+b_3}{2}-3 \\&= (x_2-1)(y_1-1)+(x_2+y_1)+ \frac{3}{2}-3\\
&=x_2y_1-\frac{1}{2}=A(\mathcal{Q})-\frac{1}{2}
\end{align*}
となるので，$A(\mathcal{P})=\frac{1}{2}$となる．
この補題を使うと，ピックの公式を証明するには以下の補題を示せばよい．
（第2段） 斜辺以外の辺が座標軸に平行である直角三角形$\mathcal{P}$についてピックの公式が成り立つことを示す．便宜上このような三角形を特殊格子三角形}という． そのような直角三角形は（第1段）の長方形$\mathcal{Q}$を対角線$L$で切り取ることで得られる．
（第3段）いま，格子三角形$\mathcal{P}$があったとき，その頂点の座標をO$=(0,0)$, A$=(x_1,y_1)$, B$=(x_2,y_2)$とし，$0 < y_1, 0 \leq y_2 \leq y_1, 0 \leq x_1$としてよい（平行移動，$x$軸と$y$軸について対称に動かせばよい）． これを
- (i) $x_2 \leq 0$または$x_1 \leq x_2$の場合
- (ii) $0 \lt x_2 \lt x_1$の場合
補題 6.3
平面上の格子多角形$\mathcal{P}$のに対し，$\mathcal{P}$は$2i(\mathcal{P})+b(\mathcal{P})-2$個の空三角形の貼り合わせで得られる．
証明
$i=i(\mathcal{P})$と$b=b(\mathcal{P})$とする．
まず$i=0$の場合を$b$についての帰納法で証明する．
なお$b \geq 3$である．$b=3$のとき，$\mathcal{P}$は空三角形であるので，補題が成り立つ．
$b>3$とする．このとき，$\mathcal{P}$の境界に含まれる２個の格子点を適当に選んで，それらを結ぶ線分$L$がその両端を除いて$\mathcal{P}$の内部に含まれるようにする．このとき，$\mathcal{P}$は$L$によって格子多角形$\mathcal{P}_1$と$\mathcal{P}_2$に分離される．帰納法の仮定より$\mathcal{P}_1$は$b(\mathcal{P}_1)-2$個，$\mathcal{P}_2$は$b(\mathcal{P}_2)-2$個の空三角形の貼り合わせとなり，$\mathcal{P}$は$b(\mathcal{P}_1)+b(\mathcal{P}_2)-4=(b+2)-4=b-2$個の空三角形の貼り合わせとなる．
次に$i>0$とし，$i$に関する帰納法を使う． いま，$\mathcal{P}$の内部に含まれる格子点$v^*$を1つ固定する． このとき，$\mathcal{P}$の境界上の点$v$と$w$を適当に選べば，$v^*$と$v$を結ぶ線分$L_1$がその両端を除いて$\mathcal{P}$の内部に含まれ，$v^*$と$w$を結ぶ線分$L_2$がその両端を除いて$\mathcal{P}$の内部に含まれるようにできる．このとき，$\mathcal{P}$は線分$L_1$と$L_2$によって格子多角形$\mathcal{P}_1$と$\mathcal{P}_2$に分離される．$i(\mathcal{P}_1),i(\mathcal{P}_2) < i$なので，帰納法の仮定より$\mathcal{P}_1$は$2i(\mathcal{P}_1)+b(\mathcal{P}_1)-2$個，$\mathcal{P}_2$は$2i(\mathcal{P}_2)+b(\mathcal{P}_2)-2$個の空三角形の貼り合わせとなる． 特に，$\mathcal{P}$は$2(i(\mathcal{P}_1)+i(\mathcal{P}_2))+(b(\mathcal{P}_1)+b(\mathcal{P}_2))-4$個の空三角形の貼り合わせである． いま，線分$L_1$と$L_2$に含まれている両端以外の格子点の個数をそれぞれ$c_1$と$c_2$とする． すると，$\mathcal{P}$の内部に含まれている格子点の個数は$i=i(\mathcal{P}_1)+i(\mathcal{P}_2)+c_1+c_2+1$となる．一方，$\mathcal{P}$の境界に含まれている格子点の個数は$b=b(\mathcal{P}_1)+b(\mathcal{P}_2)-2(c_1+c_2+1)-2$となる． 以上から$\mathcal{P}$は \begin{align*} &2(i(\mathcal{P}_1)+i(\mathcal{P}_2))+(b(\mathcal{P}_1)+b(\mathcal{P}_2))-4\\&=2(i(\mathcal{P}_1)+i(\mathcal{P}_2)+c_1+c_2+1)+(b(\mathcal{P}_1)+b(\mathcal{P}_2)-2(c_1+c_2+1)-2)-2\\&=2i+b-2 \end{align*} 個の空三角形の貼り合わせとなることがわかり，証明が完了した．
次に$i>0$とし，$i$に関する帰納法を使う． いま，$\mathcal{P}$の内部に含まれる格子点$v^*$を1つ固定する． このとき，$\mathcal{P}$の境界上の点$v$と$w$を適当に選べば，$v^*$と$v$を結ぶ線分$L_1$がその両端を除いて$\mathcal{P}$の内部に含まれ，$v^*$と$w$を結ぶ線分$L_2$がその両端を除いて$\mathcal{P}$の内部に含まれるようにできる．このとき，$\mathcal{P}$は線分$L_1$と$L_2$によって格子多角形$\mathcal{P}_1$と$\mathcal{P}_2$に分離される．$i(\mathcal{P}_1),i(\mathcal{P}_2) < i$なので，帰納法の仮定より$\mathcal{P}_1$は$2i(\mathcal{P}_1)+b(\mathcal{P}_1)-2$個，$\mathcal{P}_2$は$2i(\mathcal{P}_2)+b(\mathcal{P}_2)-2$個の空三角形の貼り合わせとなる． 特に，$\mathcal{P}$は$2(i(\mathcal{P}_1)+i(\mathcal{P}_2))+(b(\mathcal{P}_1)+b(\mathcal{P}_2))-4$個の空三角形の貼り合わせである． いま，線分$L_1$と$L_2$に含まれている両端以外の格子点の個数をそれぞれ$c_1$と$c_2$とする． すると，$\mathcal{P}$の内部に含まれている格子点の個数は$i=i(\mathcal{P}_1)+i(\mathcal{P}_2)+c_1+c_2+1$となる．一方，$\mathcal{P}$の境界に含まれている格子点の個数は$b=b(\mathcal{P}_1)+b(\mathcal{P}_2)-2(c_1+c_2+1)-2$となる． 以上から$\mathcal{P}$は \begin{align*} &2(i(\mathcal{P}_1)+i(\mathcal{P}_2))+(b(\mathcal{P}_1)+b(\mathcal{P}_2))-4\\&=2(i(\mathcal{P}_1)+i(\mathcal{P}_2)+c_1+c_2+1)+(b(\mathcal{P}_1)+b(\mathcal{P}_2)-2(c_1+c_2+1)-2)-2\\&=2i+b-2 \end{align*} 個の空三角形の貼り合わせとなることがわかり，証明が完了した．