8回目：ピックの公式の高次元化：エルハート理論
一般次元の凸多面体を考える．凸多面体$\mathcal{P} \subset \mathbb{R}^d$が格子凸多面体であるとは，すべての頂点が格子点，つまり$\mathbb{Z}^d$の点となるときにいう．よって格子凸多角形とは$2$次元格子凸多面体のことである．以降，$\mathcal{P}$の次元は空間$\mathbb{R}^d$と同じで$d$次元とする．このとき，$\mathcal{P}$はfull-dimensionalであるという．また${\rm int}(\mathcal{P}), \partial \mathcal{P}, {\rm vol}(\mathcal{P})$でそれぞれ$\mathcal{P}$の内部，境界，体積を表すことにする．$4$次元以上の体積，境界，内部を定義することはこの講義ではしないが，$3$次元の立体で想像して貰えば十分である．ただし，full-dimensionalを仮定する理由は，そうしないと${\rm int}(\mathcal{P})=\emptyset, {\rm vol}(\mathcal{P})=0$となってしまうからである．ピックの公式は$xy$平面内の$2$次元格子凸多面体の「体積」を「境界」と「内部」に属する格子点をそれぞれ数え上げることで求まるというものである．（ピックの公式は$\mathbb{R}^2$内の格子多角形の体積にのみ成り立つ公式であるが，相対体積というものを考えれば高次元でも成り立つ）．ではピックの公式のように，格子凸多面体の境界と内部に属する格子点をそれぞれ数え上げるだけでその体積は求まるのであろうか．実は，$3$次元以上ではこれは不可能である．
例 8.1
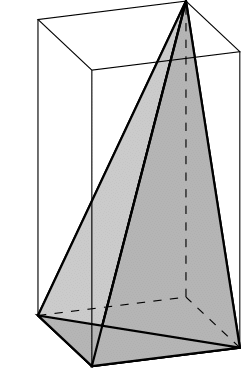
自然数$m \geq 1$に対し，$\mathcal{P}_m \subset \mathbb{R}^3$を格子点
\[
(0,0,0), (1,0,0), (0,1,0), (1,1,m)
\]
を頂点とする格子凸多面体とする．つまり下図のような四面体を考える．このとき，$\mathcal{P}_m$の境界に属する格子点は$4$つの頂点のみで，内部に格子点は存在しない．つまり，$m$の値によらず，境界と内部に属する格子点の個数は一定である．しかし，$\mathcal{P}_m$の体積は$\frac{m}{6}$で，$m$の値に依存する．つまり，境界と内部に属する格子点の個数だけでは体積が一意に定まらないことがわかる．
例 8.2
下図のような格子正方形$\mathcal{P}$を考える．
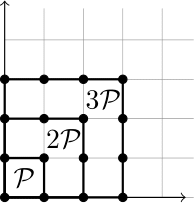すると，
\[
L_{\mathcal{P}}(1)=4, L_{\mathcal{P}}(2)=9, L_{\mathcal{P}}(3)=16, \ldots, L_{\mathcal{P}}(n)=(n+1)^2, \ldots
\]
となる．
この例では，$L_{\mathcal{P}}(n)$は$2$次の多項式で表すことができる．エルハートはどんな格子凸多面体も$L_{\mathcal{P}}(n)$を多項式として表せることを証明した．
定理 8.3 (エルハート)
$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し，
$L_{\mathcal{P}}(n)$は変数$n$に関する$d$次多項式で表せる．特に定数項は$1$である．
この多項式$L_{\mathcal{P}}(n)$を$\mathcal{P}$のエルハート多項式と呼ぶ．実はこの多項式から体積を計算することができる．
系 8.4
$L_{\mathcal{P}}(n)$の$d$次の係数，つまり$n^d$の係数は$\mathcal{P}$の体積と一致する．
証明
正の整数$n$に対し，
\[
\left(\frac{\mathbb{Z}}{n} \right)^d= \left\{ \left(\frac{a_1}{n},\ldots,\frac{a_d}{n} \right) : a_i \in \mathbb{Z} \right\}
\]
とすると，
\[
|n\mathcal{P} \cap \mathbb{Z}^d|= \left|\mathcal{P} \cap \left(\frac{\mathbb{Z}}{n} \right)^d \right|
\]
であることは容易にわかる．
$\mathcal{P} \cap (\mathbb{Z}/n)^d$の各格子点を中心に長さ$1/n$の立方体を作り，その体積の和をとると
\[
\left(\frac{1}{n}\right)^d \cdot L_{\mathcal{P}}(n)
\]
となる．
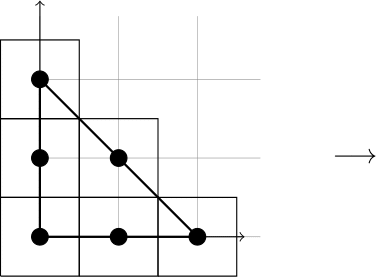
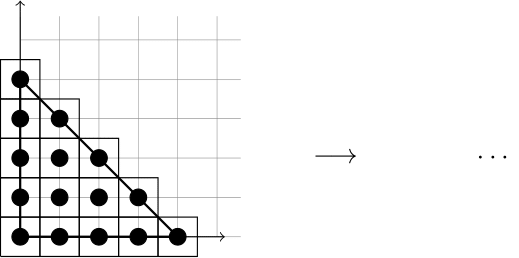ここで長さ$1/n$の$d$次元超立方体の体積は$\left(\frac{1}{n}\right)^d$である．特に，$n \to \infty$を考えることで，
\[
\mbox{$\mathcal{P}$の体積}=\lim_{n \to \infty} \left(\frac{1}{n}\right)^d \cdot L_{\mathcal{P}}(n)
\]
が成り立つ（小さな立方体で$\mathcal{P}$を埋め尽くすと考えれば理解できるであろう．より詳しくは区分求積法で示す）．$L_{\mathcal{P}}(n)$は$n$に関する$d$次多項式であったので，右辺は結局$L_{\mathcal{P}}(n)$の$n^d$の係数であることがわかる．
例8.2を考えると，$L_{\mathcal{P}}(n)=(n+1)=n^2+2n+1$なので，確かに$n^2$の係数は面積$1$に一致している．また例8.1のエルハート多項式は
\[
L_{\mathcal{P}_m}(n)=\frac{m}{6}n^3+n^2+\frac{12-m}{6}n+1
\]
であり，$n^3$の係数は体積$m/6$に一致している．
凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し，${\rm int}(\mathcal{P})$で$\mathcal{P}$の内部を表すことにする． 膨らました格子凸多面体の内部に含まれる格子点の個数はエルハート多項式から計算することができる．
定理 8.5 (エルハート--マグドナルド相互法則)
$\mathcal{P} \subset \mathbb{R}^d$を$d$次元格子凸多面体とする．
このとき，任意の$n=1,2,3,\ldots$に対し，
\[
|{\rm int}(n\mathcal{P}) \cap \mathbb{Z}^d| = (-1)^d L_{\mathcal{P}} (-n)
\]
が成り立つ．
この性質を使うとピックの公式が得られるので，エルハート多項式はピックの公式の一般化となっている．
最後に，ピックの公式と近い形で，一般の体積の公式を書いておく．
定理 8.6 (Hegedüs--Kasprezyk)
$d$次元格子凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し，
\[
{\rm vol}(\mathcal{P})=\frac{1}{d!} \sum_{m=0}^N (-1)^{N-m} \left( \binom{d}{N-m}+(-1)^d \binom{d}{N+m} \right)
\left( \left|{\rm int}(m\mathcal{P}) \cap \mathbb{Z}^d\right|+\frac{1}{2} \left| \partial(m\mathcal{P}) \cap \mathbb{Z}^d \right| \right)
\]
である．ただし，$N$は$d/2$の小数点の切り上げ，$|{\rm int}(0\mathcal{P}) \cap \mathbb{Z}^d|=1, |\partial(0\mathcal{P}) \cap \mathbb{Z}^d|=1$とする．