3回目：単項式順序と割り算アルゴリズム
この節では多項式の割り算を考える．まずは$n=1$，つまり１変数の場合の多項式の割り算を思い出す．例 3.1
$x^2+3x+5$を$x+1$で割ることを考える．
このとき，
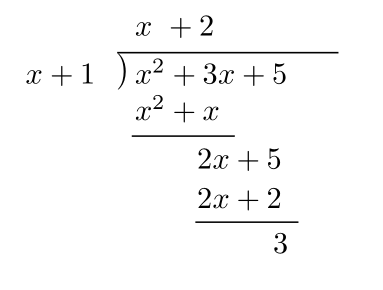となるから商が$x+2$，余りが$3$となる．つまり$x^2+3x+5=(x+2)(x+1)+3$と書き表せる．この筆算の最初のステップは元となる多項式$x^2+3x+5$の最高次の項$x^2$を，割る多項式$x+1$に単項式$x$を掛けたものを引くことで消し，次数の下がった多項式を得る．得られた次数の下がった多項式に対して同様のステップを繰り返すことで，最終的に残った多項式の次数が割る多項式の次数より小さくなり，ステップは終了する．
この例のように，多項式$f,g \in k[x]$に対し，$f$を$g$で割るということは，$f=qg+r$を満たす，「単純な多項式」 $q,r \in k[x]$を見つけることである．より正確に述べると次の命題が成り立つ．
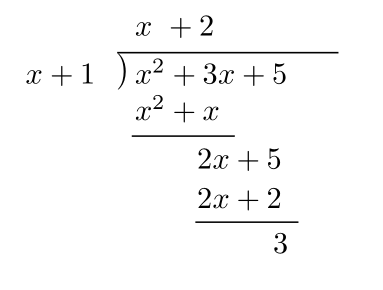
命題 3.2 (割り算アルゴリズム（1変数）)
$g \in k[x]$をゼロでない多項式とする．
このとき，任意の$f \in k[x]$は
\[
f=qg+r
\]
と書き表せる．ここで，$q,r \in k[x]$で，$r=0$または$\deg(r) < \deg(g)$が成り立つ．
さらに$q$と$r$は一意的に定まる．
証明
$q$と$r$を求めるアルゴリズムの擬似コードを書くだけに止める．（このアルゴリズムが停止することと，得られた結果が命題を満たすことの証明は省略する）．多項式$f \in k[x]$に対し，${\rm LT}(f)$を$f$の最高次の項とする．
\begin{eqnarray*}
&&\hbox{Input} : g,\, f\\
&&\hbox{Output} : q, r\\[-4pt]
\\[-4pt]
&&q := 0;\, r := f\\
&&\hbox{WHILE}\ r \neq 0\ \hbox{AND}\ {\rm LT}(g)\mbox{が}{\rm LT}(r)\mbox{を割り切る}\ \hbox{DO}\\
&&\qquad\quad q := q + {\rm LT}(r)/{\rm LT}(g)\\
&&\qquad\quad r := r - ({\rm LT}(r)/{\rm LT}(g))\, g\\
&&\hbox{RETURN}\ q,r
\end{eqnarray*}
それでは変数が増えた場合はどうか．
多項式$f \in k[X]$を$f_1,\ldots,f_s \in k[X]$で割るというのは，$f=q_1 f_1 + \cdots + q_s f_s +r$を満たす，「単純な多項式」 $q_1,\ldots,q_s, r \in k[X]$を見つけることである．これを１変数の場合のアルゴリズムのように，高い次数を打ち消し合うアルゴリズムを作り行いたい．
しかし，１変数の場合と違って，多変数の場合，多項式内に同じ次数の項が存在する場合がある．例えば，$x^2+y^2$の$x^2$と$y^2$はともに次数$2$の項である．この場合，どっちの項を優先して消せばいいのか，という問題が出てくる．多変数の多項式における割り算を定式化するために，まずは単項式全体に順序を付ける．
定義 3.3
$\Sigma$を集合とし，「$\leq$」を$\Sigma$上で定義された二項関係とする．つまりある$\Sigma \times \Sigma$の部分集合$X$が存在して，$(a,b) \in X$ならば$a \leq b$と書く．このとき，$\leq$が$\Sigma$上の半順序 (partial order) であるとは，以下の３条件を満たすときをいう．
$a \leq b$かつ$a \neq b$のときは$a < b$と書く．さらに任意の$a,b \in \Sigma$に対し，$a \leq b$または$b \leq a$を満たすとき，半順序$\leq$は全順序 (total order) と呼ばれる．
例 3.4
$\Sigma$を集合$\{ a,b,c \}$の冪集合とし，$X \subseteq Y$ならば$X \leq Y$と書くことにすると，$\leq$は$\Sigma$上の半順序である．しかし，全順序ではない．実際，$\{a\}$と$\{b\}$は比較不可能である．
定義 3.5
$\mathcal{M}_n$を$k[X]$の単項式全体の集合とし，$\leq $を$\mathcal{M}_n$上の全順序とする．このとき，$\leq$が$k[X]$の単項式順序 (monomial order) であるとは，次の２条件を満たすときをいう．
$x^{\alpha} \leq x^{\beta}$のとき，$\alpha \leq \beta$と書くこともある．
例を挙げる前に，まずは補題を2つ紹介する．
補題 3.6
$\leq$を$k[X]$上の単項式順序とする．
このとき，任意の$u,v \in \mathcal{M}_n$に対し，$u$が$v$を割り切るならば$u \leq v$である．
証明
$u$が$v$を割り切ると仮定する．このとき，ある$w \in \mathcal{M}_n$が存在して，$v=wu$となる．また単項式順序の定義より$1 \leq w$となる．したがって，再び単項式順序の定義より$1 \cdot u \leq w \cdot u=v$となり，$u \leq v$がわかる．
補題 3.7
$\leq$を$k[X]$の単項式順序とする．このとき，$\leq$に関する単項式の無限減少列
\[
u_0 > u_1 > u_2 > \cdots \ \ \ \ \ (u_i \in \mathcal{M}_n)
\]
は存在しない．
証明
証明略．
代表的な単項式順序を３つ紹介する．
以下，$u=x^{\alpha}, v=x^{\beta}$を単項式とする．
例 3.8 (辞書式順序)
$u,v$に対し，$u <_{\rm lex} v$をベクトル$\beta-\alpha$において最も左にある$0$でない成分が正となる，で定義する．
例えば，$v=x_1^2 x_2$と$u=x_1 x_2 x_3$を考えると$\beta-\alpha=(2,1,0)-(1,1,1)=(1,0,-1)$なので$x_1^2 x_2 >_{\rm lex} x_1 x_2 x_3$である．
このとき，$<_{\rm lex}$は$k[X]$の単項式順序となる．
辞書式順序は辞書で使われている単語の順序に似ている．実際，ベクトル$\alpha$の成分を，単語の中の文字と見なすことができる．文字はアルファベット順に順序づけされている． \[ a > b> c > \cdots > z. \] すると，例えば，$arrow >_{\rm lex} arson$となる．これは1, 2番目の文字はどちらも同じで，3文字目が$r > s$であるからである．}
辞書式順序は辞書で使われている単語の順序に似ている．実際，ベクトル$\alpha$の成分を，単語の中の文字と見なすことができる．文字はアルファベット順に順序づけされている． \[ a > b> c > \cdots > z. \] すると，例えば，$arrow >_{\rm lex} arson$となる．これは1, 2番目の文字はどちらも同じで，3文字目が$r > s$であるからである．}
例 3.9 (次数付き辞書式順序
$u,v$に対し，$u <_{\rm glex} v$を$|\alpha| < |\beta|$，または$|\alpha|=|\beta|$かつベクトル$\beta-\alpha$において最も左にある$0$でない成分が正となる，で定義する．
例えば，$v=x_1^2 x_2$と$u=x_1 x_2 x_3^2$を考えると$x_1^2 x_2 <_{\rm glex} x_1 x_2 x_3^2$である．（一方で，$x_1^2 x_2 >_{\rm lex} x_1 x_2 x_3^2$である．）
このとき，$<_{\rm glex}$は$k[X]$の単項式順序となる．
例 3.10 (次数付き逆辞書式順序)
$u,v$に対し，$u <_{\rm rlex} v$を$|\alpha| < |\beta|$，または$|\alpha|=|\beta|$かつベクトル$\beta-\alpha$において最も右にある$0$でない成分が負となる，で定義する．
$v=x_1^2 x_2$と$u=x_1 x_2 x_3$を考えると$\beta-\alpha=(2,1,0)-(1,1,1)=(1,0,-1)$なので$x_1^2 x_2 >_{\rm rlex} x_1 x_2 x_3$である．
このとき，$<_{\rm rlex}$は$k[X]$の単項式順序となる．
辞書式順序が単項式順序となることの証明を書いておく．（他の順序に関しても，ほぼ同様に証明できる．）
命題 3.11
$\leq_{\rm lex}$は単項式順序である．
証明
単項式$1$に対応するベクトルは$(0,\ldots,0)$であるため，任意の$u \in \mathcal{M}_n$に対し，$1 \leq_{\rm lex} u$となることは明らかである．
次に$u,v \in \mathcal{M}_n$を任意にとり，$u \leq_{\rm lex} v$であるとする．このとき，任意の$w=x^{\gamma} \in \mathcal{M}_n$に対し，$uw$と$vw$を定義に従って比較すると， \[ (\beta+\gamma)-(\alpha+\gamma)=\beta-\alpha \] となるので，$uw \leq_{\rm lex} vw$が従う．
以上より$\leq_{\rm lex}$は単項式順序である．
単項式順序に関連していくつか用語を準備する．
次に$u,v \in \mathcal{M}_n$を任意にとり，$u \leq_{\rm lex} v$であるとする．このとき，任意の$w=x^{\gamma} \in \mathcal{M}_n$に対し，$uw$と$vw$を定義に従って比較すると， \[ (\beta+\gamma)-(\alpha+\gamma)=\beta-\alpha \] となるので，$uw \leq_{\rm lex} vw$が従う．
以上より$\leq_{\rm lex}$は単項式順序である．
定義 3.12
$f=\sum_{\alpha} a_{\alpha} x^{\alpha} \in k[X]$をゼロでない多項式とし，$<$を$k[X]$の単項式順序とする．
$f$の$<$に関する多重次数 (multidegree) とは$f$の中で$<$に関して最大の項$x^{\alpha}$の指数ベクトル，$\alpha$のことである．これを${\rm mdeg}(f)$と書く．
$f$の$<$に関する先頭係数 (leading coefficient) とは，${\rm LC}(f)=a_{{\rm mdeg}(f)}$のことである．
$f$の$<$に関する先頭単項式 (leading monomial) とは${\rm LM}(f)=x^{{\rm mdeg}(f)}$のことである．
$f$の$<$に関する先頭項 (leading term)とは${\rm LT}(f)={\rm LC}(f) \cdot {\rm LM (f)}$のことである．
それでは，多変数の多項式の割り算を定式化する．
定理 3.13 (割り算アルゴリズム (多変数))
$k[X]$の単項式順序$<$を１つ固定し，$F=(f_1,\ldots,f_s)$を$k[X]$の順序付けられた$s$個の多項式の組とする．このとき，任意の$f \in k[X]$は
\[
f=q_1f_1+\cdots+q_sf_s +r
\]
と書ける．ここで，$q_1,\ldots,q_s,r \in k[X]$で$r=0$，または$r=\sum_{\alpha} a_{\alpha} x^{\alpha}$で，どの単項式$x^{\alpha} (a_{\alpha} \neq 0)$も${\rm LM}(f_1),\ldots,{\rm LM}(f_s)$のいずれでも割り切れない．この$r$を，$f$を$F$で割った余り (remainder) と呼ぶ．さらに，もし$q_if_i \neq 0$ならば，${\rm LM}(f) \geq {\rm LM}(q_if_i)$である．
証明
１変数の場合と同様に，アルゴリズムの擬似コードを書いて終わりとする．
\begin{eqnarray*}
&&\hbox{Input} : f_{1},\ldots,f_{s},\,f\\
&&\hbox{Output} : q_{1},\ldots,q_{s},r\\[-4pt]
\\[-4pt]
&&q_1 :=0; \ldots; q_{s} :=0; r :=0\\
&&p:=f\\
&&\hbox{WHILE}\ p\neq 0\ \hbox{DO}\\
&&\qquad\qquad i:=1\\
&&\qquad\qquad \mathit{divisionoccurred}:= \hbox{\sf false}\\
&&\qquad\qquad \hbox{WHILE}\ i\leq s\ \hbox{AND}\ \mathit{divisionoccurred}=
\hbox{\sf false}\ \hbox{DO}\\
&&\qquad\qquad\qquad \hbox{IF}\ {\rm LT}(\,f_{i})\mbox{が}
{\rm LT}(\hskip.8pt p)\mbox{を割り切る} \ \hbox{THEN}\\
&&\qquad\qquad\qquad\qquad\qquad q_{i}:=q_{i}+{\rm LT}(\hskip.8pt p)/{\rm LT}(\,f_{i})\\
&&\qquad\qquad\qquad\qquad\qquad p:=p-({\rm LT}(\hskip.8pt p)/{\rm LT}(\,f_{i}))\hskip1.5pt f_{i}\\
&&\qquad\qquad\qquad\qquad\qquad \mathit{divisionoccurred}:=\hbox{\sf true}\\
&&\qquad\qquad\qquad \hbox{ELSE}\\
&&\qquad\qquad\qquad\qquad\qquad i:=i+1\\
&&\qquad\qquad \hbox{IF}\ \mathit{divisionoccurred}=\hbox{\sf false}\ \hbox{THEN}\\
&&\qquad\qquad\qquad r:=r+{\rm LT}(\hskip.8pt p)\\
&&\qquad\qquad\qquad p:=p-{\rm LT}(\hskip.8pt p)\\
&&\hbox{RETURN}\ q_{1},\ldots,q_{s},r
\end{eqnarray*}
例 3.14
割り算アルゴリズムの例として，
$f=x^2y+xy^2+y^2$を$f_1=xy-1$と$f_2=y^2-1$で割ろう．ここで単項式順序として$x >_{\rm lex} y$となる辞書式順序を考える．このとき，${\rm LT}(f_1)=xy,{\rm LT}(f_2)=y^2$であり，$f$の中にはこのどちらかで割り切れる項がある．$f_1,f_2$と$q_1,q_2$を筆算の中で縦に並べて考えると次のようになる．
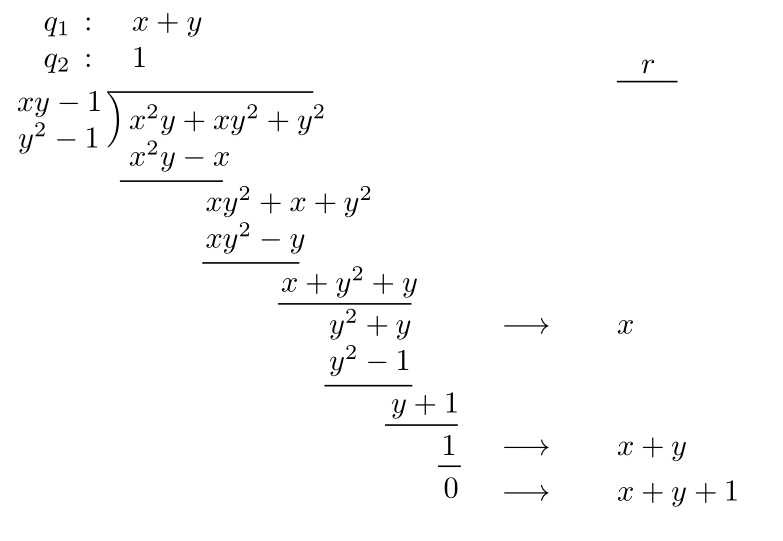この結果より，$f$は次のように表せる．
\[
f=(x+y) \cdot (xy-1) + 1 \cdot (y^2-1)+(x+y+1).
\]
この余りの項はどれもが${\rm LT}(f_1)$でも${\rm LT}(f_2)$でも割り切れない．
このアルゴリズムの残念な点が１つある．それは余りが$f_1,\ldots,f_s$の順序付けに依存してしまう点である．実際，次の例を見る．
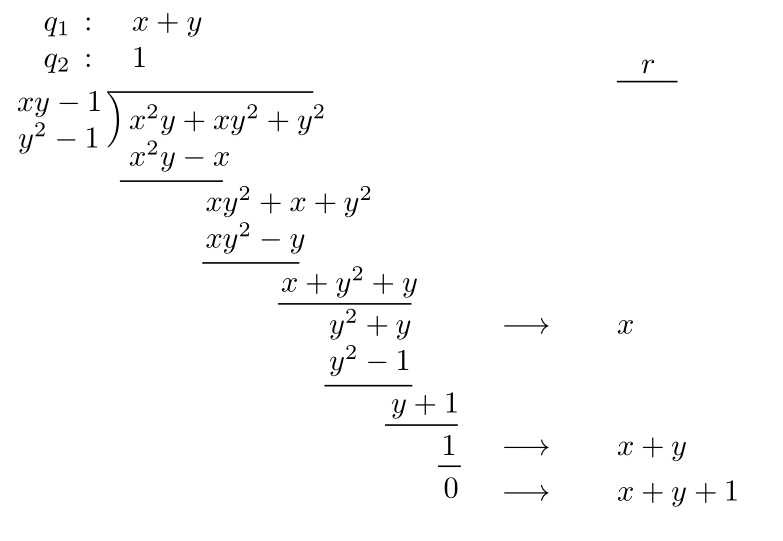
例 3.15
$f_1=xy-1, f_2=y^2-1 \in k[x,y]$とおき，$x >_{\rm lex} y$となる辞書式順序を考える．$f=xy^2-x$を$F=(f_1,f_2)$で割ると，結果は
\[
f=y \cdot (xy-1) + 0 \cdot (y^2-1) + (-x+y)
\]
となる．$F=(f_2,f_1)$に対しては，
\[
f=x \cdot (y^2-1) + 0 \cdot (xy-1) + 0
\]
となる．
$f$の$F=(f_1,\ldots,f_s)$による割り算を行って，余りが$r=0$となったとき，$f \in \langle f_1,\ldots,f_s \rangle$である．つまり，$r=0$は$f$がイデアルに属するための十分条件である．しかし上の例のように必要条件ではない．イデアル所属問題への応用の点から見てもこの割り算アルゴリズムは不完全である．次の章ではこの問題を改善する．