2回目：面
空間$\mathbb{R}^N$の超平面 (hyperplane)とは$\mathbf{a} \in \mathbb{R}^N$と実数$b$を使い， \[ \mathcal{H}=\{ \mathbf{x} \in \mathbb{R}^N : \langle \mathbf{a} , \mathbf{x} \rangle =b \} \] と表示される集合$\mathcal{H} \subset \mathbb{R}^N$のことである．ただし，$\mathbf{a} \neq (0,\ldots,0)$である． $\mathbb{R}^N$の超平面は次元$N-1$のアフィン空間である． 逆にどんな$N-1$次元アフィン空間も$\mathbb{R}^N$の超平面である． また空間$\mathbb{R}^N$の部分集合 \begin{align*} \mathcal{H}^{(+)} &= \{ \mathbf{x} \in \mathbb{R}^N : \langle \mathbf{a} , \mathbf{x} \rangle \geq b \},\\ \mathcal{H}^{(-)} &= \{ \mathbf{x} \in \mathbb{R}^N : \langle \mathbf{a} , \mathbf{x} \rangle \leq b \} \end{align*} を超平面$\mathcal{H}$が定義する閉半空間という．例 2.1
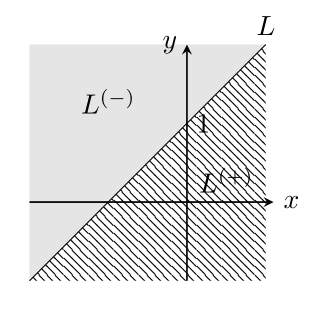
$xy$平面において，直線$L:y=x+1$を考えると，この直線は
\[
L=\{ (x,y) \in \mathbb{R}^2 : \langle (1, -1) , (x,y) \rangle = -1 \}
\]
と表記できるので，$\mathbb{R}^2$の超平面である．また閉半空間$L^{(+)}$と$L^{(-)}$は下図のようになる．
前節では凸多面体を凸閉包を使って定義したが，閉半空間を用いても定義できる．
実際，
定理 2.2
空間$\mathbb{R}^N$の有限個の閉半空間$\mathcal{H}_1^{(+)},\ldots,\mathcal{H}_s^{(+)}$の共通部分
\[
\mathcal{P} = \bigcap_{i=1}^s \mathcal{H}_i^{(+)}
\]
は$\mathbb{R}^N$の空でない有界集合であれば，凸多面体である．逆に任意の凸多面体は有限個の閉半空間の共通部分である．
例 2.3
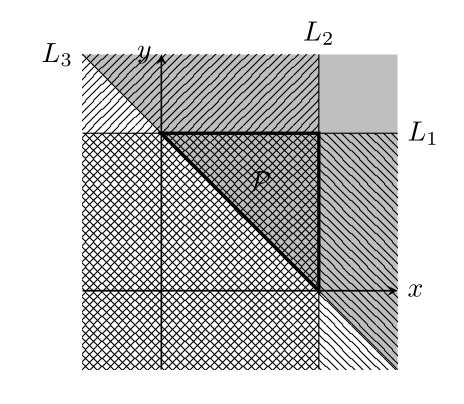
$\mathcal{P} \subset \mathbb{R}^2$を$(1,1), (1,0), (0,1)$を頂点とする三角形とし，3つの直線
\begin{align*}
L_1&=\{ (x,y) \in \mathbb{R}^2 : \langle (0,-1), (x,y) \rangle = -1 \},\\
L_2&=\{ (x,y) \in \mathbb{R}^2 : \langle (-1,0), (x,y) \rangle = -1 \},\\
L_3&=\{ (x,y) \in \mathbb{R}^2 : \langle (1,1), (x,y) \rangle = 1 \}\\
\end{align*}
を考えると，$\mathcal{P} = \bigcap_{i=1}^3 L_i^{(+)}$である（下図参照）．
凸多面体$\mathcal{P} \subset \mathbb{R}^N$の支持超平面 (supporting hyperplane)とは，次の条件を満たす空間$\mathbb{R}^N$の超平面$\mathcal{H}$のことである：
例 2.4
例 2.3の三角形を考えると，直線$L_1,L_2,L_3$は$\mathcal{P}$の支持超平面となっている．
さらに
\begin{align*}
L_4&=\{ (x,y) \in \mathbb{R}^2 : \langle (1,1), (x,y) \rangle = 2 \},\\
L_5&=\{ (x,y) \in \mathbb{R}^2 : \langle (1,1), (x,y) \rangle = 1.5 \},\\
L_6&=\{ (x,y) \in \mathbb{R}^2 : \langle (1,1), (x,y) \rangle = 0.5 \}
\end{align*}
を考えると，$L_4$は支持超平面であるが，$L_5$と$L_6$は支持超平面ではない（下図参照）．
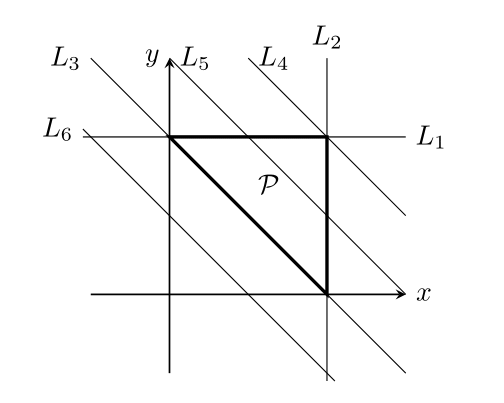
支持超平面は凸集合であるので，$\mathcal{P} \cap \mathcal{H}$もまた凸集合である．特に，これは凸多面体である．
命題 2.5
$\mathcal{P} \subset \mathbb{R}^N$を凸多面体とし，部分集合$V \subset \mathbb{R}^N$は$\mathcal{P} = {\rm conv}(V)$を満たすとする．$\mathcal{H} \subset \mathbb{R}^N$が$\mathcal{P}$の支持超平面であれば，$\mathcal{P} \cap \mathcal{H} = {\rm conv} ( V \cap \mathcal{H})$である．
この凸多面体と支持超平面の共通部分を面という．
定義 2.6
$\mathcal{P} \subset \mathbb{R}^N$を$d$次元凸多面体とし，$\mathcal{H}$を$\mathcal{P}$の支持超平面とする．このとき，$\mathcal{F}=\mathcal{P} \cap \mathcal{H}$を$\mathcal{P}$の面 (face)という．特に，$\dim \mathcal{F}=i$のとき，$i$面といい，$0$面のことを頂点 (vertex)，$1$面のことを辺 (edge)，
$(d-1)$面のことをファセット (facet)という．
補足 2.7
第1節でも凸多面体の頂点を定義したが，1点集合である$0$面を$\mathbb{R}^N$の点と同一視すればこの2つの定義は一致する．つまり，凸多面体$\mathcal{P}$の$0$面全体の和集合$V$は$\mathcal{P}={\rm conv}(V)$となる最小の有限集合である．
凸閉包を用いた凸多面体の定義では，頂点がその凸多面体を与えていた．
閉半空間を用いた定義では，ファセットがその凸多面体を与える．
定理 2.8
凸多面体$\mathcal{P} \subset \mathbb{R}^N$のファセット全体を$\mathcal{F}_1,\ldots,\mathcal{F}_s$とする．それぞれの$\mathcal{F}_i$に対応する$\mathcal{P}$の支持超平面を$\mathcal{H}_i$（つまり$\mathcal{P} \cap \mathcal{H}_i= \mathcal{F}_i$である）とし$\mathcal{P} \subset \mathcal{H}_i^{(+)}$であるとする．このとき，
\[
\mathcal{P} = \left( \bigcap_{i=1}^s \mathcal{H}_i^{(+)}\right) \cap {\rm aff}(\mathcal{P})
\]
である．特に，上の式から$\mathcal{H}_i^{(+)}$を1つでも取り除くと等式は成り立たない．
さらにファセットは凸多面体の境界の構造を与える．
凸多面体$\mathcal{P} \subset \mathbb{R}^N$の（相対）境界 ((relative) boundary)とは，距離空間$\mathbb{R}^N$の部分距離空間${\rm aff}(\mathcal{P})$における$\mathcal{P}$の境界のことである．$\mathcal{P}$の境界を$\partial \mathcal{P}$と書く．
定理 2.9
凸多面体$\mathcal{P} \subset \mathbb{R}^N$の境界$\partial \mathcal{P}$は$\mathcal{P}$のファセットの和集合と一致する．
最後に面が満たす諸性質を述べる．
命題 2.10
$\mathcal{P} \subset \mathbb{R}^N$を凸多面体とし，$\mathcal{F},\mathcal{F}'$を$\mathcal{P}$の面とする．
このとき，
$\mathcal{F}$が$\mathcal{F}'$の面であることを$\mathcal{F} \prec \mathcal{F}'$と書き，便宜上，空集合も自分自身も面であるとする（つまり$\emptyset \prec \mathcal{F}$と$\mathcal{F} \prec \mathcal{F}$が成り立つ）．
この命題から，$\mathcal{P}$の面全体の集合は$\prec$により半順序関係（反射律，反対称律，推移律を満たす）となる．特に，束（どの2要素も上限，下限を持つ）である．これを面束 (face lattice)という．２つの凸多面体は，それぞれの面束が順序同型のとき，組合せ的同型 (combinatorially isomorphic)であるという．
$d$次元凸多面体$\mathcal{P} \subset \mathbb{R}^N$とアフィン変換$\phi : \mathbb{R}^N \to \mathbb{R}^N$に対し，$\mathcal{F}$が$\mathcal{P}$の
$i$面であれば，$\phi(\mathcal{F})$は$\phi(\mathcal{P})$の$i$面であり，$\mathcal{P}$と$\phi(\mathcal{P})$は組合せ的同型となる．
したがって，以前と同じ議論により，凸多面体の面を調べるときは$N=d$としてよい．