3回目：オイラーの多面体定理
$xyz$空間の凸多面体$\mathcal{P} \subset \mathbb{R}^3$の頂点，辺，面の個数をそれぞれ$v,e,f$とすると，$v-e+f=2$が成り立つというのが$3$次元のオイラーの多面体定理であった．この定理を任意の次元まで一般化し，$3$次元も含めて証明する．まず凸多面体の面が有限個しかないことは命題 2.5から従う． そこで$d$次元凸多面体$\mathcal{P} \subset \mathbb{R}^N$に対し，$f_i(\mathcal{P})$で$\mathcal{P}$の$i$面の個数を表し，数列 \[ f(\mathcal{P})=(f_0(\mathcal{P}),f_1(\mathcal{P}),\ldots,f_{d-1}(\mathcal{P})) \] を$\mathcal{P}$の$f$列 ($f$-vector)という． どの多面体か明らかの時は，$f_i=f_i(\mathcal{P})$と書く． 例えば，$3$単体$\mathcal{P}$の$f$列は \[ f(\mathcal{P})=(4,6,4) \] である． より一般に，$d$単体の$f$列は次のように計算できる．
命題 3.1
$d$単体$\mathcal{P} \subset \mathbb{R}^N$の$f$列$f(\mathcal{P})=(f_0,f_1,\ldots,f_{d-1})$に対し，
\[
f_i=\binom{d+1}{i+1}
\]
が全ての$0 \leq i \leq d-1$で成り立つ．ここで，$\binom{n}{k}$は二項係数$\frac{n!}{k!(n-k)!}$のことである．
証明
$\mathcal{P}$の頂点集合を$V$とし，部分集合$W \subset V$で$|W|=d=|V|-1$となるものを固定する．簡単のため，$N=d$とし，さらに
平行移動により，$V \setminus W=\{ \mathbf{0}\}$と仮定してよい．このとき$\mathbf{0} \notin {\rm aff}(W)$であり，${\rm aff}(W)$は超平面であるので，ある$\mathbf{a} \in \mathbb{R}^d$を使って
\[
\mathcal{H}:={\rm aff}(W)=\{ \mathbf{x} \in \mathbb{R}^d : \langle \mathbf{a}, \mathbf{x} \rangle =1\}
\]
と書くことができる．
$W \subset \mathcal{H}$かつ$\mathbf{0} \in \mathcal{H}^{(+)}$なので，$\mathcal{H}$は$\mathcal{P}$の支持超平面である．特に，$\mathcal{H} \cap V= W$なので，${\rm conv}(W)$は$\mathcal{P}$の
ファセットである．この事実と命題 2.10を使えば，帰納法によって，$V$から$i+1$個の点を選んだ集合を$V'$とすると，${\rm conv}(V')$は$\mathcal{P}$の$i$面となることが証明できる．
よって$\mathcal{P}$の$i$面の個数は$d+1$点から$i+1$点を選ぶ方法と一致するので，欲しい等式が得られた．
一般に，凸多面体の$f$列を計算することは非常に困難である．しかし，$f$列が満たすべき様々な関係式が知られている．そのうちの1つがオイラーの多面体定理である．
定理 3.2 (オイラーの多面体定理)
次元$d \geq 2$の凸多面体$\mathcal{P} \subset \mathbb{R}^N$の$f$列
\[
f(\mathcal{P})=(f_0,f_1,\ldots,f_{d-1})
\]
は等式
\begin{equation}
f_0-f_1+f_2-\cdots+(-1)^{d-1} f_{d-1} = 1 + (-1)^{d-1} \cdots\cdots (1)
\end{equation}
を満たす．
定理の証明のために1つ補題を準備する．
補題 3.3
次元$d \geq 2$の凸多面体$\mathcal{P} \subset \mathbb{R}^d$に対し，超平面$\mathcal{H} \subset \mathbb{R}^d$で条件
「超平面$\mathcal{H}$をどのように平行移動させても$\mathcal{P}$の頂点を$2$個以上含むことはできない」
を満たすものが存在する．
証明
空間$\mathbb{R}^d$の異なる2点$\mathbf{y}$と$\mathbf{z}$を通過する直線$L_{\mathbf{y},\mathbf{z}}$と直交し，原点を通過する超平面を$\mathcal{H}'_{\mathbf{y},\mathbf{z}}$とする．
このとき，$L_{\mathbf{y},\mathbf{z}}$を含む平面$\mathcal{H}_{\mathbf{y},\mathbf{z}}$の法線ベクトル$\mathbf{a} \in \mathbb{R}^d$は$\mathcal{H}'_{\mathbf{y},\mathbf{z}}$に属する．
すると，$\mathcal{P} \subset \mathbb{R}^d$の頂点を$\mathbf{a}_1,\ldots,\mathbf{a}_v$とし
\[
\mathbb{R}^d \setminus \bigcup_{1 \leq i < j \leq v} \mathcal{H}'_{\mathbf{a}_i,\mathbf{a}_j} \neq \emptyset
\]
に属する任意の$\mathbf{a}'$を選び，$\mathbf{a}'$を法線ベクトルとする超平面を$\mathcal{H} \subset \mathbb{R}^d$とすれば，$\mathcal{H}$は条件を満たす．
定理 3.2の証明
$N=d$としてよい．次元$d$に関する数学的帰納法を使う．
$xy$平面の凸多角形の頂点の個数$f_0$と辺の個数$f_1$は一致するので，$d=2$ならば等式(1)は成立する．
$d \geq 3$を仮定する．$v=f_0(\mathcal{P})$とし，$\mathcal{P}$の頂点を$\mathbf{a}_1,\ldots,\mathbf{a}_v$とする．さらに補題 3.3の条件を満たす超平面$\mathcal{H} \subset \mathbb{R}^d$を固定する． 今，超平面$\mathcal{H}_1,\ldots,\mathcal{H}_{2v-1}$を次のようにとる：
$1 \leq i \leq v$に対し，$\mathcal{H}_{2i-1}$は$\mathcal{H}$に平行で$\mathbf{a}_i \in \mathcal{H}_{2i-1}$である．さらに頂点の番号を適当に並べ替えることで，$\mathcal{H}_{2i-1}$は$\mathcal{H}_{2i-3}$と$\mathcal{H}_{2i+1}$の間に位置するようにする．
$1 \leq i \leq v-1$に対し，$\mathcal{H}_{2i}$は$\mathcal{H}$に平行で$\mathcal{H}_{2i-1}$と$\mathcal{H}_{2i+1}$の間に位置するようにとる．
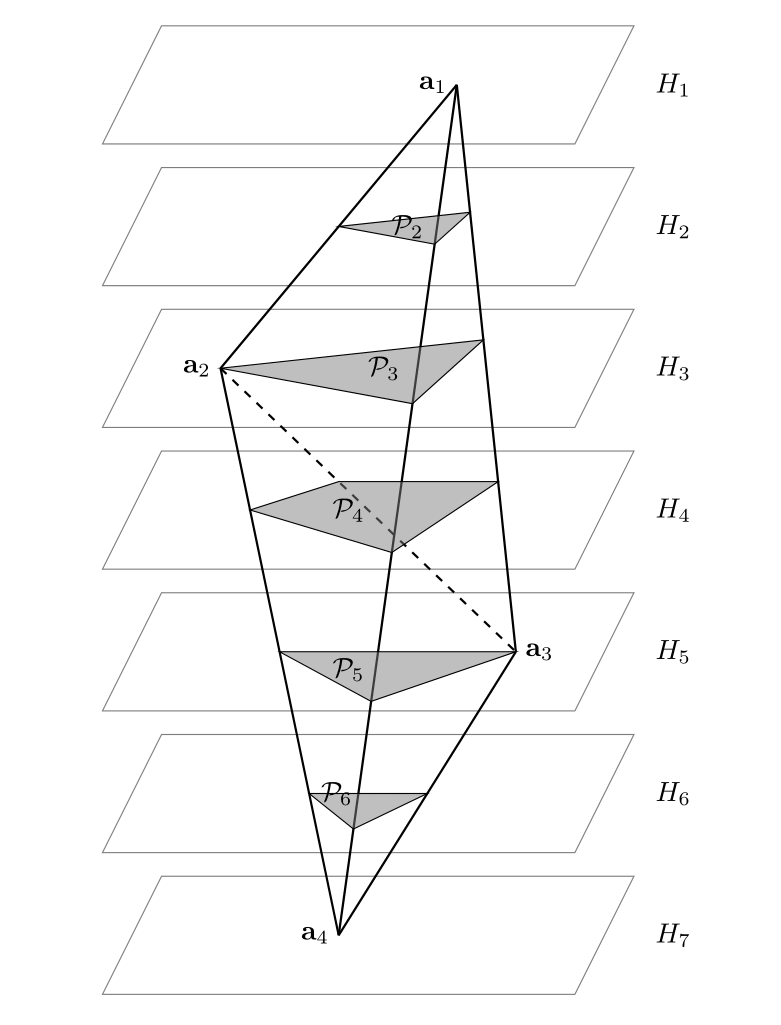すると$\mathcal{H}_{1}$と$\mathcal{H}_{2v-1}$は$\mathcal{P}$の支持超平面であり，
\[
\mathcal{P}_1=\mathcal{H}_1 \cap \mathcal{P} =\{ \mathbf{a}_1\}, \ \ \ \ \mathcal{P}_{2v-1}=\mathcal{H}_{2v-1} \cap \mathcal{P} = \{\mathbf{a}_v\}
\]
となる．一方，
\[
\mathcal{P}_2=\mathcal{H}_2 \cap \mathcal{P} , \mathcal{P}_3=\mathcal{H}_3 \cap \mathcal{P} ,\ldots,\mathcal{P}_{2v-2}=\mathcal{H}_{2v-2} \cap \mathcal{P}
\]
は次元$d-1$の凸多面体である．
$\mathcal{P}$のそれぞれの$j$面$\mathcal{F}^{j}$（ただし$1 \leq j \leq d-1$）とそれぞれの$\mathcal{P}_i$（ただし$2 \leq i \leq 2v-2$）に対し，$\psi(\mathcal{F}^j,\mathcal{P}_i)$を \[ \psi(\mathcal{F}^j,\mathcal{P}_i)=\begin{cases} 0, & (\mathcal{P}_i \cap {\rm int}(\mathcal{F}^j) = \emptyset)\\ 1, & (\mathcal{P}_i \cap {\rm int}(\mathcal{F}^j) \neq \emptyset) \end{cases} \] と定義する． 面$\mathcal{F}^j$の頂点を含む$\mathcal{H}_i$のうち，添字$i$が最も小さくなるものを$\alpha$とし，最も大きくなるものを$\beta$とする．このとき，$\alpha$と$\beta$は奇数である．これを$\alpha=2m-1$と$\beta=2 \ell -1$とおくと，$i=2m,2m+1,\ldots,2\ell-2$のとき，しかもそのときに限り，$\mathcal{P}_i \cap {\rm int}(\mathcal{F}^{j}) \neq \emptyset$であり，$\mathcal{P}_i \cap \mathcal{F}^j$は$\mathcal{P}_i$の$(j-1)$面となる． 特に，$\psi(\mathcal{F}^j,\mathcal{P}_i)=1$となる添字$i$で偶数のものの個数は，添字$i$で奇数のものの個数よりもちょうど$1$個多い． すると， \[ \sum_{i=2}^{2v-2} (-1)^i \psi (\mathcal{F}_j,\mathcal{P}_i)=1 \] となる．よって \[ \sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \left( \sum_{i=2}^{2v-2}(-1)^i \psi(\mathcal{F}^j,\mathcal{P}_i) \right) = f_j(\mathcal{P}) \] すると， \begin{equation} \label{eq:euler2} \sum^{d-1}_{j=1}(-1)^j \left(\sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \left( \sum_{i=2}^{2v-2}(-1)^i \psi(\mathcal{F}^j,\mathcal{P}_i) \right) \right)= \sum_{j=1}^{d-1}(-1)^j f_j(\mathcal{P})\cdots\cdots (2) \end{equation} である． したがって，この等式の左辺が$1+(-1)^{d-1}-f_0(\mathcal{P})$であることを示せばよい．
まず \[\sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \psi(\mathcal{F}^j,\mathcal{P}_i)=\begin{cases} f_0(\mathcal{P}_i)-1, &\mbox{($i$は奇数で$j=1$)}\\ f_{j-1}(\mathcal{P}_i), &\mbox{(その他)} \end{cases}\] である．実際，
$i$が偶数ならば$\mathcal{P}_i$の$(j-1)$面は，$\mathcal{P}$の$j$面と$\mathcal{H}_i$の共通部分である，
$i$が奇数で$j>1$ならば，$\mathcal{P}_i$の$(j-1)$面は$\mathcal{P}$の$j$面と$\mathcal{H}_i$との共通部分である，
$i$が奇数ならば，$\mathcal{P}_i$の1つの頂点は$\mathcal{P}$の頂点であり，残りの頂点は$\mathcal{P}$の辺と$\mathcal{H}_i$との共通部分である，
という事実から従う． よって帰納法の仮定を$\mathcal{P}_i$に使うことで， \begin{align*} \sum_{j=1}^{d-1} (-1)^j \left( \sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \psi(\mathcal{F}^j,\mathcal{P}_i) \right) &=\begin{cases} \sum^{d-1}_{j=1}(-1)^j f_{j-1}(\mathcal{P}_i) +1, &\mbox{($i$は奇数)}\\ \sum^{d-1}_{j=1}(-1)^j f_{j-1}(\mathcal{P}_i), &\mbox{($i$は偶数)} \end{cases} \\ &=\begin{cases} -(1+(-1)^{d-2}) +1, &\mbox{($i$は奇数)}\\ -(1+(-1)^{d-2}), &\mbox{($i$は偶数)} \end{cases} \\ &=\begin{cases} (-1)^{d-1}, &\mbox{($i$は奇数)}\\ (-1)^{d-1}-1, &\mbox{($i$は偶数)} \end{cases} \end{align*} となる． すると， \begin{align*} \mbox{(2)の左辺} &=\sum_{i=2}^{2v-2}(-1)^i \left( \sum^{d-1}_{j=1}(-1)^j \left(\sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \psi(\mathcal{F}^j,\mathcal{P}_i) \right) \right) \\ &=(-1)^{d-1}-(v-1)=(-1)^{d-1}+1-f_0(\mathcal{P}) \end{align*} となり，等式(1)が成り立つ．
$\mathcal{P}$のそれぞれの$j$面$\mathcal{F}^{j}$（ただし$1 \leq j \leq d-1$）とそれぞれの$\mathcal{P}_i$（ただし$2 \leq i \leq 2v-2$）に対し，$\psi(\mathcal{F}^j,\mathcal{P}_i)$を \[ \psi(\mathcal{F}^j,\mathcal{P}_i)=\begin{cases} 0, & (\mathcal{P}_i \cap {\rm int}(\mathcal{F}^j) = \emptyset)\\ 1, & (\mathcal{P}_i \cap {\rm int}(\mathcal{F}^j) \neq \emptyset) \end{cases} \] と定義する． 面$\mathcal{F}^j$の頂点を含む$\mathcal{H}_i$のうち，添字$i$が最も小さくなるものを$\alpha$とし，最も大きくなるものを$\beta$とする．このとき，$\alpha$と$\beta$は奇数である．これを$\alpha=2m-1$と$\beta=2 \ell -1$とおくと，$i=2m,2m+1,\ldots,2\ell-2$のとき，しかもそのときに限り，$\mathcal{P}_i \cap {\rm int}(\mathcal{F}^{j}) \neq \emptyset$であり，$\mathcal{P}_i \cap \mathcal{F}^j$は$\mathcal{P}_i$の$(j-1)$面となる． 特に，$\psi(\mathcal{F}^j,\mathcal{P}_i)=1$となる添字$i$で偶数のものの個数は，添字$i$で奇数のものの個数よりもちょうど$1$個多い． すると， \[ \sum_{i=2}^{2v-2} (-1)^i \psi (\mathcal{F}_j,\mathcal{P}_i)=1 \] となる．よって \[ \sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \left( \sum_{i=2}^{2v-2}(-1)^i \psi(\mathcal{F}^j,\mathcal{P}_i) \right) = f_j(\mathcal{P}) \] すると， \begin{equation} \label{eq:euler2} \sum^{d-1}_{j=1}(-1)^j \left(\sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \left( \sum_{i=2}^{2v-2}(-1)^i \psi(\mathcal{F}^j,\mathcal{P}_i) \right) \right)= \sum_{j=1}^{d-1}(-1)^j f_j(\mathcal{P})\cdots\cdots (2) \end{equation} である． したがって，この等式の左辺が$1+(-1)^{d-1}-f_0(\mathcal{P})$であることを示せばよい．
まず \[\sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \psi(\mathcal{F}^j,\mathcal{P}_i)=\begin{cases} f_0(\mathcal{P}_i)-1, &\mbox{($i$は奇数で$j=1$)}\\ f_{j-1}(\mathcal{P}_i), &\mbox{(その他)} \end{cases}\] である．実際，
という事実から従う． よって帰納法の仮定を$\mathcal{P}_i$に使うことで， \begin{align*} \sum_{j=1}^{d-1} (-1)^j \left( \sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \psi(\mathcal{F}^j,\mathcal{P}_i) \right) &=\begin{cases} \sum^{d-1}_{j=1}(-1)^j f_{j-1}(\mathcal{P}_i) +1, &\mbox{($i$は奇数)}\\ \sum^{d-1}_{j=1}(-1)^j f_{j-1}(\mathcal{P}_i), &\mbox{($i$は偶数)} \end{cases} \\ &=\begin{cases} -(1+(-1)^{d-2}) +1, &\mbox{($i$は奇数)}\\ -(1+(-1)^{d-2}), &\mbox{($i$は偶数)} \end{cases} \\ &=\begin{cases} (-1)^{d-1}, &\mbox{($i$は奇数)}\\ (-1)^{d-1}-1, &\mbox{($i$は偶数)} \end{cases} \end{align*} となる． すると， \begin{align*} \mbox{(2)の左辺} &=\sum_{i=2}^{2v-2}(-1)^i \left( \sum^{d-1}_{j=1}(-1)^j \left(\sum_{\tiny{\mbox{$\mathcal{F}^j:\mathcal{P}$の$j$面}}} \psi(\mathcal{F}^j,\mathcal{P}_i) \right) \right) \\ &=(-1)^{d-1}-(v-1)=(-1)^{d-1}+1-f_0(\mathcal{P}) \end{align*} となり，等式(1)が成り立つ．