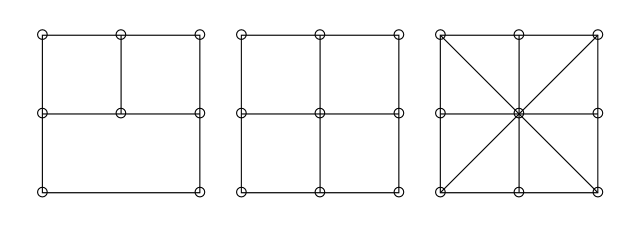
4回目：三角形分割
凸多面体$\mathcal{P} \subset \mathbb{R}^N$に対し，$\mathcal{P}$の細分 (subdivision) $\mathcal{S}$ とは，凸多面体からなる有限集合で条件
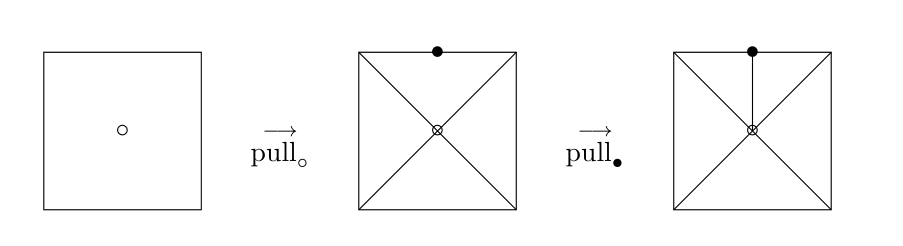
(操作) $\mathbf{m}$を含まない$\Delta$の面$\Delta'$に対し，角錐${\rm conv}(\Delta' \cup \{\mathbf{m}\})$を考え，このようにして得られた角錐の集合$\{{\rm conv}(\Delta' \cup \{\mathbf{m}\})\}_{\mathbf{m} \notin \Delta' \prec \Delta}$と$\Delta$を$\mathcal{S}$の中で取り替える．
この操作を全ての$\mathbf{m}$を含む$\mathcal{S}$の面で行い，得られた集合を${\rm pull}_{\mathbf{m}} \mathcal{S}$と書く． このとき${\rm pull}_{\mathbf{m}} \mathcal{S}$は次の2種類の凸多面体からなる集合である：
(P1) $\Delta \in \mathcal{S}$かつ$\mathbf{m} \notin \Delta$ならば$ \Delta \in {\rm pull}_{\mathbf{m}} \mathcal{S}$．
(P2) $\Delta' \prec \Delta \in \mathcal{S}$かつ$\mathbf{m} \in \Delta \setminus \Delta' $ならば${\rm conv}(\Delta' \cup \{\mathbf{m}\}) \in {\rm pull}_{\mathbf{m}} \mathcal{S}$．
この${\rm pull}_{\mathbf{m}} \mathcal{S}$は$\mathcal{P}$の細分となっており，$\mathcal{S}$の$\mathbf{m}$に関する強引き戻し細分 (strong pulling subdivision)という．
定理 4.1
$\mathcal{P} \subset \mathbb{R}^N$を凸多面体とし$\mathcal{S}$をその細分とする．$M=(\mathbf{m}_1,\ldots,\mathbf{m}_r)$を
$\mathcal{S}$の頂点を全て含む，順番付けられた$\mathcal{P}$の点の集合とする．
各$1 \leq i \leq r$に対し，
\[
\mathcal{S}_i := {\rm pull}_{\mathbf{m}_i} \mathcal{S}_{i-1}
\]
と定義する．ただし，$\mathcal{S}_0:=\mathcal{S}$である．このとき，$\mathcal{S}':=\mathcal{S}_r$は$\mathcal{P}$の三角形分割である．
証明
$\mathcal{S}'$の各セルが単体であることを示せばよい．
$\mathbf{m}$を含む${\rm pull}_{\mathbf{m}} \mathcal{S}$の各面は$\mathbf{m}$を頂上とする角錐である．もし$\Delta \in \mathcal{S}$が$\mathbf{m'}$を頂上とする角錐であれば，${\rm pull}_{\mathbf{m}} \mathcal{S}$の中で$\Delta$の内側にあり，さらに$\mathbf{m'}$を含む各面はまだ$\mathbf{m'}$を頂上とする角錐である．
以上から，$M$に含まれるすべての点に関して強引き戻しした細分$\mathcal{S}'$の各セル$\mathcal{C} \in \mathcal{S}'$とその各頂点$\mathbf{v} \in \mathcal{C}$に対し，$\mathcal{C}$が$\mathbf{v}$を頂上とする角錐となることがわかる．これは$\mathcal{S}'$の各セルが単体であることを意味する．
オイラーの多面体定理のように，三角形分割の面の数え上げに関してもある等式が成り立つ．
$d$次元凸多面体$\mathcal{P}$の三角形分割$\mathcal{T}$に対し，$f_i(\mathcal{T})$で$\mathcal{T}$に属する$i$面の個数を表し，数列
\[
f(\mathcal{T})=(f_0(\mathcal{T}),f_1(\mathcal{T}),\ldots,f_d(\mathcal{T}))
\]
を$\mathcal{T}$の$f$列と呼ぶ．
また$\partial \mathcal{T}:=\{ \mathcal{F} \in \mathcal{T} : \mathcal{F} \subset \partial \mathcal{P}\}$は$\mathcal{P}$の境界の三角形分割を与え，その$f$列\[f(\partial\mathcal{T})=(f_0(\partial \mathcal{T}),f_1(\partial \mathcal{T}),\ldots,f_{d-1}(\partial \mathcal{T}))\]も考えることができる．
このとき，$\mathcal{T}$の被約オイラー標数を
\[
\widetilde{\chi}(\mathcal{T})=\sum_{i=-1}^{d} (-1)^i f_i(\mathcal{T})
\]
で定義し，$\mathcal{T}$の境界の被約オイラー標数を
\[
\widetilde{\chi}(\partial \mathcal{T})=\sum_{i=-1}^{d-1} (-1)^{i} f_i(\partial \mathcal{T})
\]
で定義する．ただし$f_{-1}(\mathcal{T})=f_{-1}(\partial \mathcal{T})=1$とする．これは空集合に対応している．
驚くべきことに，三角形分割の取り方によらず．上記2つの被約オイラー標数は一定である．
定理 4.2
$d$次元凸多面体$\mathcal{P} \subset \mathbb{R}^N$と$\mathcal{P}$の三角形分割$\mathcal{T}$に対し，
\[\begin{aligned}
\widetilde{\chi}(\mathcal{T})&=0,\\
\widetilde{\chi}(\partial\mathcal{T})&=(-1)^{d-1}
\end{aligned}\]
が成り立つ．
この結果は代数的位相幾何学のよく知られているものだが，この講義では本筋から外れるため，証明で用いる道具の紹介で止める．
体$k$を固定し，三角形分割$\mathcal{T}$の頂点集合を$V=\{x_1,x_2,\ldots,x_v\}$とする． 以降，$\mathcal{T}$の各面$\mathcal{F}={\rm conv}(x_{i_1},\ldots,x_{i_r})$はその頂点集合$\{x_{i_1},\ldots,x_{x_r}\}$と同一視して議論する． まず$\mathcal{T}$のすべての$i$面の集合を基底とする$k$上線型空間を \[ C_i=C_i(\mathcal{T};k) \] で表す．つまり，$C_i$はそれぞれの$i$面を形式的に文字だと思い，その文字を変数とした$k$係数$1$次斉次多項式全体と$0$からなる線型空間である． ただし，$C_{-1}$は$\{\emptyset\}$を基底とする$1$次元線型空間である． 一方，$i < -1$または$i > d$のとき，$C_i=(0)$である． 今，線型写像 \[ \partial_i : C_i \to C_{i-1} \] を以下のように定義する：線型空間$C_i$の基底の元$\sigma$の頂点が \[ x_{\ell_0},x_{\ell_1},\ldots,x_{\ell_i}, \ \ \ \ 1 \leq \ell_0 < \ell_1 < \cdots < \ell_i \leq v \] であるとき，$\partial_i(\sigma)$を \[ \partial_i(\sigma)=\sum_{j=0}^i (-1)^j (\sigma \setminus \{ x_{\ell_j}\}) \] で定義する（$\sigma \setminus \{ x_{\ell_j}\}$は$(i-1)$面なので，$C_{i-1}$の基底であることに注意）． すると線型空間と線形写像の列 \[ \cdots \to (0) \overset{\partial_{d+1}}{\to} C_{d} \overset{\partial_{d}}{\to} C_{d-1} \overset{\partial_{d-1}}{\to} \cdots \overset{\partial_{2}}{\to} C_1 \overset{\partial_{1}}{\to} C_0 \overset{\partial_{0}}{\to} C_{-1} \overset{\partial_{-1}}{\to} (0) \to \cdots \] が得られる． このとき，具体的な計算により次の補題が得られる．
補題 4.3
任意の$i$に対し，
$\partial_{i} \circ \partial_{i+1} = 0$が成り立つ．特に，
\[
{\rm Im} (\partial_{i+1}) \subset {\rm Ker} (\partial_i) \subset C_i
\]
である．
この補題により，線型商空間
\[
\widetilde{H}_i(\mathcal{T}; k ) := {\rm Ker} (\partial_i) / {\rm Im} (\partial_{i+1})
\]
が定義でき，これを$\mathcal{T}$の$k$上の被約ホモロジー群と呼ぶ．
この商空間の次元を使って被約オイラー標数が計算できる（というよりこちらが定義である）．
命題 4.4 (Euler-Poincaré公式)
体$k$によらず，等式
\[
\widetilde{\chi}(\mathcal{T})=\sum_{i \geq -1} (-1)^i \dim_k \widetilde{H}_i (\mathcal{T};k)
\]
が成り立つ．
証明
商空間の次元公式より
\begin{align*}
\sum_{i \geq -1}(-1)^i \dim_k \widetilde{H}_i (\mathcal{T};k)&=\sum_{i \geq -1} (-1)^i (\dim_k{\rm Ker}(\partial_i)-\dim_k{\rm Im}(\partial_{i+1}))\\
&=\sum_{i \geq -1} (-1)^i \dim_k{\rm Ker}(\partial_i)+\sum_{i \geq -1}^{d} (-1)^{i+1} \dim_k{\rm Im}(\partial_{i+1})
\\
&=\sum_{i \geq 0} (-1)^i (\dim_k{\rm Ker}(\partial_i)+\dim_k{\rm Im}(\partial_{i}))-\dim_k{\rm Ker}(\partial_{-1})\\
&=\sum_{i \geq 0} (-1)^i \dim_k C_i(\mathcal{T};k) -1\\
&=\sum_{i \geq 0} (-1) f_i(\mathcal{T}) -1=\widetilde{\chi}(\mathcal{T})
\end{align*}
となる．
$\partial \mathcal{T}$に関しても同様の議論ができる．
また三角形分割を$\mathcal{T}$を単体的$d$球体，境界の三角形分割$\partial \mathcal{T} $を単体的$d-1$球面という概念に拡張し，同様の議論を行い，
最終的に，定理 4.2は次の命題から従う．
命題 4.5
単体的$d$球体$\mathcal{B}$に対し，
\[
\widetilde{H}_i(\mathcal{B};k)=
(0),
\]
さらに単体的$d-1$球面$\mathcal{S}$に対し，
\[ \widetilde{H}_i(\mathcal{S};k)=
\begin{cases}
(0), \ \ (i \neq d-1)\\
k, \ \ \ \ (i = d-1)
\end{cases}
\]
が成り立つ．