3.1：準同型写像
それではまず，環準同型写像を定義する．定義 3.1.1
$R,S$を可換環とする．写像$f : R \to S$が（環）準同型写像 (homomorphism)であるとは，以下の3つの条件を満たすときにいう．
準同型写像の定義の(1)は$(R,+_R,0_R)$と$(S,+_S, 0_S)$をアーベル群として見れば，$f$が群準同型写像になることに他ならない．
したがって，次の性質が成り立つ．
- 任意の$x,y \in R$に対し，$f(x+_R y)=f(x) +_S f(y)$．
- 任意の$x,y \in R$に対し，$f(x\cdot_R y)=f(x) \cdot_S f(y)$．
- $f(1_R)=1_S$．
命題 3.1.2
$R,S$を可換環とし，$f:R \to S$を環準同型写像とする．
- $f(0_R)=0_S$．
- 任意の$x \in R$に対し，$f(-x)=-f(x)$．
証明
情報数理Cの5.1節を参照．
一方で，定義の(2)を考えると以下が示せる．
命題 3.1.3
$R,S$を可換環とし，
$f:R \to S$を環準同型写像とする．もし$x \in R$が$R$の単元であれば，$f(x)$は$S$の単元である．
証明
$x$が$R$の単元とすると，$x \cdot_R y =1_R$を満たす$y \in R$が存在する．
すると，$f$が準同型写像であるので，
\[
1_S=f(1_R)=f(x \cdot_R y)=f(x) \cdot_S f(y)
\]
が成り立つので，$f(x)$は$S$の単元である．
それでは準同型写像の例を見ていこう．
例 3.1.4
(1) 整数環$\mathbb{Z}$から剰余環$\mathbb{Z}/n\mathbb{Z}$の写像 $\varphi : \mathbb{Z} \to \mathbb{Z}/n\mathbb{Z}$を$\varphi(a) = \overline{a}$で定めると，$\varphi$ は環準同型写像である．
実際，任意の $a, b \in \mathbb{Z}$ に対して，
\begin{align*}
\varphi(a + b) &= \overline{a + b} = \overline{a} + \overline{b} = \varphi(a) + \varphi(b),\\
\varphi(ab) &= \overline{ab} = \overline{a} \cdot \overline{b} = \varphi(a) \cdot \varphi(b)
\end{align*}
である．
また $\varphi(1) = \overline{1}$ より，準同型写像の条件を満たす．
より一般に，可換環$R$とそのイデアル$I$に対し，写像$\varphi: R \to R/I$を$x \mapsto \overline{x}$で定めると，$\varphi$は環準同型写像となる．これを自然な（全射）準同型写像という．
(2) $\mathbb{Q}[x]$から$\mathbb{Q}$への写像$\varphi: \mathbb{Q}[x] \to \mathbb{Q}$を$f \mapsto f(1)$（多項式に1を代入）で定義すると，$\varphi$は環準同型写像である（確かめよ）．より，一般に，可換環$R$と元$a \in R$に対し，写像$\varphi : R[x] \to R$を$f \mapsto f(a)$（多項式に$a$を代入）で定義すると，$\varphi$は環準同型写像である．これを代入写像という．
(3) 単位元を保たない例として，$\mathbb{Z} \to \mathbb{Z}$ に $f(a) = 2a$ と定めた写像は加法と乗法の条件は満たすが，$f(1) = 2 \neq 1$ なので環準同型写像ではない．補足として，$\mathbb{Z}$をアーベル群として見れば，$f$は群準同型写像である．
群準同型写像のときと同様に，像と核を定義する．
より一般に，可換環$R$とそのイデアル$I$に対し，写像$\varphi: R \to R/I$を$x \mapsto \overline{x}$で定めると，$\varphi$は環準同型写像となる．これを自然な（全射）準同型写像という．
(2) $\mathbb{Q}[x]$から$\mathbb{Q}$への写像$\varphi: \mathbb{Q}[x] \to \mathbb{Q}$を$f \mapsto f(1)$（多項式に1を代入）で定義すると，$\varphi$は環準同型写像である（確かめよ）．より，一般に，可換環$R$と元$a \in R$に対し，写像$\varphi : R[x] \to R$を$f \mapsto f(a)$（多項式に$a$を代入）で定義すると，$\varphi$は環準同型写像である．これを代入写像という．
(3) 単位元を保たない例として，$\mathbb{Z} \to \mathbb{Z}$ に $f(a) = 2a$ と定めた写像は加法と乗法の条件は満たすが，$f(1) = 2 \neq 1$ なので環準同型写像ではない．補足として，$\mathbb{Z}$をアーベル群として見れば，$f$は群準同型写像である．
定義 3.1.5
$R,S$を可換環とし，$f:R \to S$を環準同型写像とする．
元$x \in R$に対し，$f(x)$を$x$の$f$に関する像という．また
集合
\[
{\rm Im}(f):=\{ f(x) : x \in R\} \subset S
\]
を$f$の像 (image)という．一方，集合
\[
{\rm Ker}(f):=\{ x \in R : f(x)=0_R\} \subset R
\]
を$f$の核 (kernel)という．
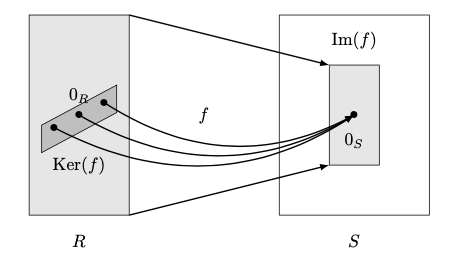
下図のように，${\rm Ker}(f)$とは加法の単位元1点に圧縮される集合のことである．
命題 3.1.6
$R,S$を可換環とし，
$f:R \to S$を環準同型写像とする．
-
${\rm Im}(f)$は$S$の部分環である．
-
${\rm Ker}(f)$は$R$のイデアルである．
証明
(1) 任意の$x,y \in {\rm Im}(f)$をとる．このとき，ある$x',y' \in R$を使って$x=f(x'), y=f(y')$と書ける．
すると$f$が準同型写像であることから
\begin{align*}
x+_S y=f(x')+_Sf(y')=f(x'+_R y'),\\
x \cdot_S y=f(x') \cdot_S f(y')=f(x' \cdot_R y')
\end{align*}
が得られ，$x'+_R y', x' \cdot_R y' \in R$なので，$x+_S y, x \cdot_S y \in {\rm Im}(f)$が従う．また$f(1_R)=1_S \in {\rm Im}(f)$である．以上より，${\rm Im}(f)$は$S$の部分環である．
(2) $f(0_R)=0_S$より$0_R \in {\rm Ker}(f)$である．任意の$x,y \in {\rm Ker}(f)$と$a \in R$をとる．このとき，$f(x)=f(y)=0_S$である．$f$が準同型写像であることから \begin{align*} f(x+_R y)=f(x)+_S f(y)=0_S +_S 0_S=0_S,\\ f(a\cdot_R x)=f(a)\cdot_S f(x)=f(a) \cdot_S 0_S=0_S\\ \end{align*} が得られるので，$x +_R y, a \cdot_R x \in {\rm Ker}(f)$が従う．以上より，${\rm Ker}(f)$は$R$のイデアルである．
また群のときと同様で，${\rm Ker}(f)$から$f$の単射性がわかる．
(2) $f(0_R)=0_S$より$0_R \in {\rm Ker}(f)$である．任意の$x,y \in {\rm Ker}(f)$と$a \in R$をとる．このとき，$f(x)=f(y)=0_S$である．$f$が準同型写像であることから \begin{align*} f(x+_R y)=f(x)+_S f(y)=0_S +_S 0_S=0_S,\\ f(a\cdot_R x)=f(a)\cdot_S f(x)=f(a) \cdot_S 0_S=0_S\\ \end{align*} が得られるので，$x +_R y, a \cdot_R x \in {\rm Ker}(f)$が従う．以上より，${\rm Ker}(f)$は$R$のイデアルである．
命題 3.1.7
$R,S$を可換環とする．
環準同型写像$f:R \to S$が単射である必要十分条件は${\rm Ker}(f)=\{0_R\}$である．
証明
情報数理Cの5.1節を参照．
最後に${\rm Ker}(f)$の例を見る．
例 3.1.8
(1) 環準同型写像$\varphi : \mathbb{Z} \to \mathbb{Z}/n\mathbb{Z}; a \mapsto \overline{a}$
に対し，
\[{\rm Ker}(f)=\{a \in \mathbb{Z}: f(a)=\overline{a}=\overline{0}\}=\{a \in \mathbb{Z} : a-0=a \in n\mathbb{Z}\}=n\mathbb{Z}\]である．一般に，自然な全射$\varphi : R \to R/I$に対し，${\rm Ker}(\varphi)=I$である．
(2) 環準同型写像$\varphi: \mathbb{Q}[x] \to \mathbb{Q};f \mapsto f(1)$に対し，\[ {\rm Ker}(\varphi) = \{ f(x) \in \mathbb{Q}[x] : f(1) = 0 \} \] である．これは，$x=1$ を代入して $0$ になる多項式全体の集合であり，明らかに $x - 1$ を因数にもつ多項式の集合と一致する．したがって， \[ {\rm Ker}(\varphi) = \langle x - 1 \rangle=\{ (x-1)g(x) : g(x) \in \mathbb{Q}[x]\} \] である．このように，代入写像の核は対応する代入点を根にもつ多項式の生成するイデアルとなる．
(2) 環準同型写像$\varphi: \mathbb{Q}[x] \to \mathbb{Q};f \mapsto f(1)$に対し，\[ {\rm Ker}(\varphi) = \{ f(x) \in \mathbb{Q}[x] : f(1) = 0 \} \] である．これは，$x=1$ を代入して $0$ になる多項式全体の集合であり，明らかに $x - 1$ を因数にもつ多項式の集合と一致する．したがって， \[ {\rm Ker}(\varphi) = \langle x - 1 \rangle=\{ (x-1)g(x) : g(x) \in \mathbb{Q}[x]\} \] である．このように，代入写像の核は対応する代入点を根にもつ多項式の生成するイデアルとなる．